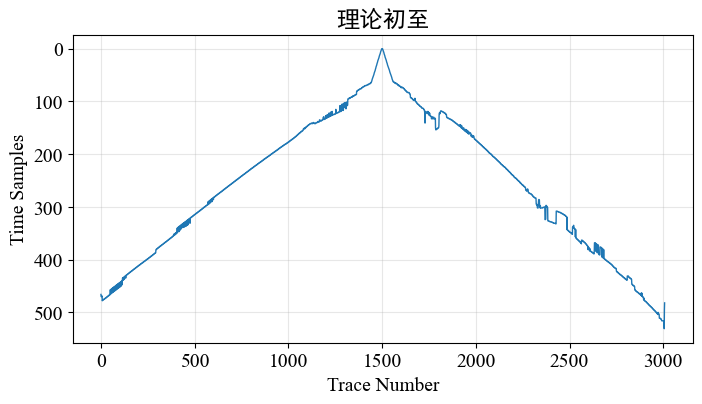
有时在研究过程中，需要用到理论正演数据的初至，如果手动拾取的话…想想都头大，本文提供一种计算理论正演地震数据初至的方法。

1. 数据准备

首先，准备一下数据，去SEG Open data下载一个2D Walkaway VSP的正演数据。

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import read_segy
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

#for font in fm.fontManager.ttflist: # 查看可用字体
#    print(font.name)
matplotlib.rcParams['font.family'] = ['Times New Roman', 'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

看下数据长啥样：（其中read_segy可以参考这篇笔记：Python读写segy数据）

1
2
3
4
5
6
7
model_vsp =  read_segy.read_segy(data_dir='F:/data/SEAM_I_Walkaway_VSP/SEAM_Well1VSP_Shots23900.sgy',shotnum=0)
print(model_vsp.shape)
print(model_vsp.min())
print(model_vsp.max())

plt.figure(figsize=(10,6))
plt.imshow(model_vsp[0],vmin=-10,vmax=10,aspect=1)

vsp_data

2. 计算初至的函数

定义计算初至的函数,思路为找到超过该道最大振幅值*相对阈值的第一个点。

(一开始是计划找到不为0的第一个点，但是会受到一些随机噪声的影响，故放弃)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def calculate_fb(seismic_data, threshold=0.01):
    """
    计算理论地震数据的first break
    
    参数:
    seismic_data: 输入地震数据[单炮],shape为(n_time_samples, n_traces)
    threshold: 相对阈值
    """
    def _find_first(arr):
        """找到第一个超过相对阈值的点"""
        max_val = np.max(np.abs(arr))
        if max_val == 0:
            return -1
        thresholds = max_val * threshold
        above_threshold_indices = np.where(np.abs(arr) > thresholds)[0]
        return above_threshold_indices[0] if len(above_threshold_indices) > 0 else -1
    
    # 计算原始值
    fb_raw = np.apply_along_axis(_find_first, axis=0, arr=seismic_data)
    
    # 前向填充-1
    fb = fb_raw.copy()
    for i in range(1, len(fb)):
        if fb[i] == -1:
            fb[i] = fb[i-1]
    
    # 处理开头的-1
    if fb[0] == -1:
        first_valid = next((x for x in fb if x != -1), 0)
        fb[0] = first_valid
    
    return fb

3. 计算单炮的初至，检查结果

计算该数据第0炮的初至，并画图看看：

1
2
3
4
5
6
7
8
9
10
11
12
13
fb = calculate_fb(model_vsp[0],threshold=0.01)

plt.figure(figsize=(10, 6))
plt.plot(fb, linewidth=1)
plt.title('初至')
plt.xlabel('Trace Number')
plt.ylabel('Time Samples')
plt.gca().invert_yaxis()
plt.grid(True, alpha=0.3)
plt.show()

print(f"First Break shape = : {fb.shape}")
print(f"First Break range = : {np.min(fb)} - {np.max(fb)}")

vsp_fb

检查一下单道的拾取位置是否正确

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 检查其中4道吧
threshold = 0.01 * np.max(np.abs(model_vsp[0]))
plt.figure(figsize=(12, 10))

# 检查第0道
plt.subplot(2, 2, 1)
plt.plot(model_vsp[0, :, 0])
plt.axhline(y=threshold, color='b', linestyle='--', label=f'Threshold: {threshold}')
plt.axvline(x=fb[0], color='r', linestyle='--', label='First above threshold')
plt.title('trace 0')
plt.legend()

# 检查第500道
plt.subplot(2, 2, 2)
plt.plot(model_vsp[0, :, 500])
plt.axhline(y=threshold, color='b', linestyle='--', label=f'Threshold: {threshold}')
plt.axvline(x=fb[500], color='r', linestyle='--', label='First above threshold')
plt.title('trace 500')
plt.legend()

# 检查第1000道
plt.subplot(2, 2, 3)
plt.plot(model_vsp[0, :, 1000])
plt.axhline(y=threshold, color='b', linestyle='--', label=f'Threshold: {threshold}')
plt.axvline(x=fb[1000], color='r', linestyle='--', label='First above threshold')
plt.title('trace 1000')
plt.legend()

# 检查第1500道
plt.subplot(2, 2, 4)
plt.plot(model_vsp[0, :, 1500])
plt.axhline(y=threshold, color='b', linestyle='--', label=f'Threshold: {threshold}')
plt.axvline(x=fb[1500], color='r', linestyle='--', label='First above threshold')
plt.title('trace 1000')
plt.legend()

plt.rcParams['font.size'] = 14
plt.tight_layout()
plt.show()

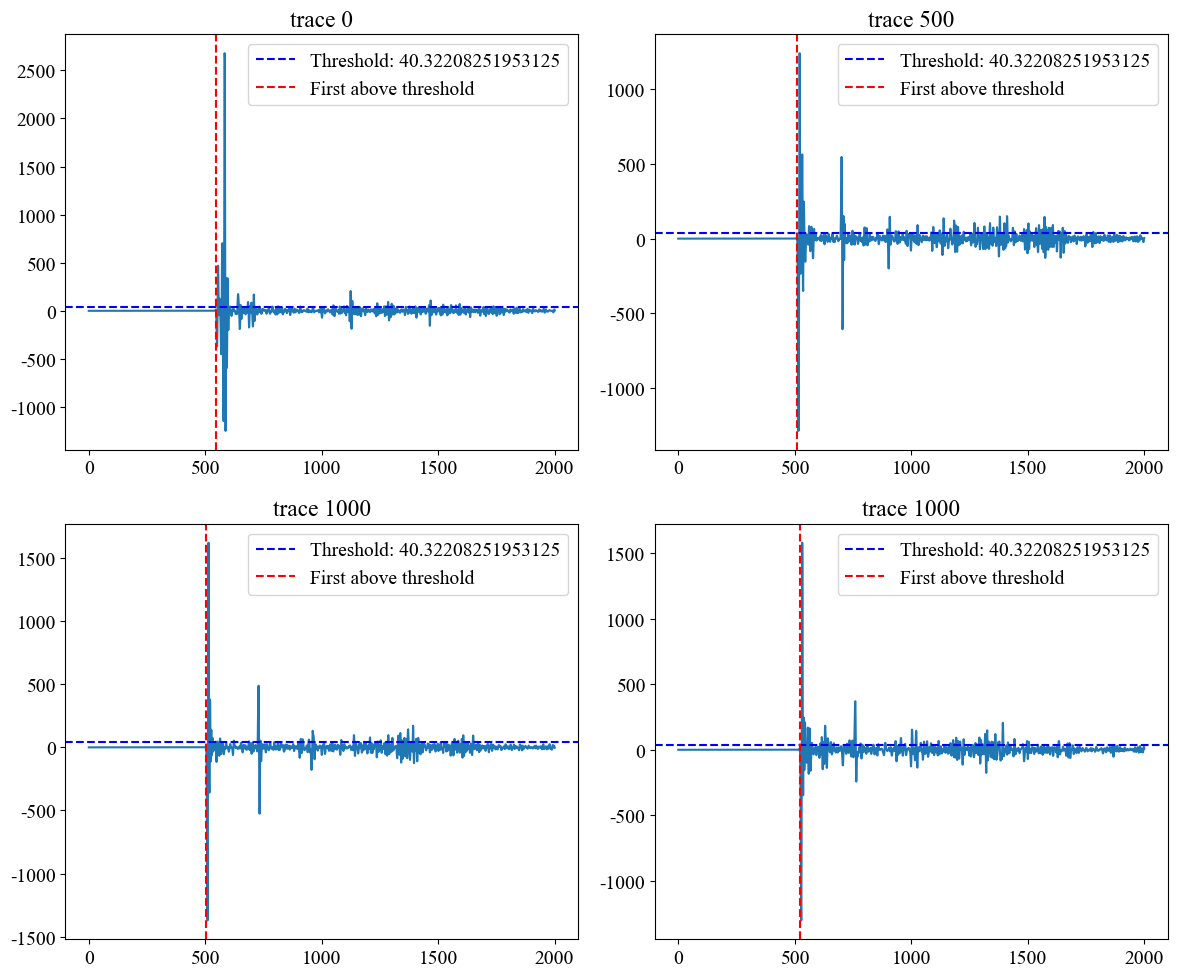
vsp_fb_check

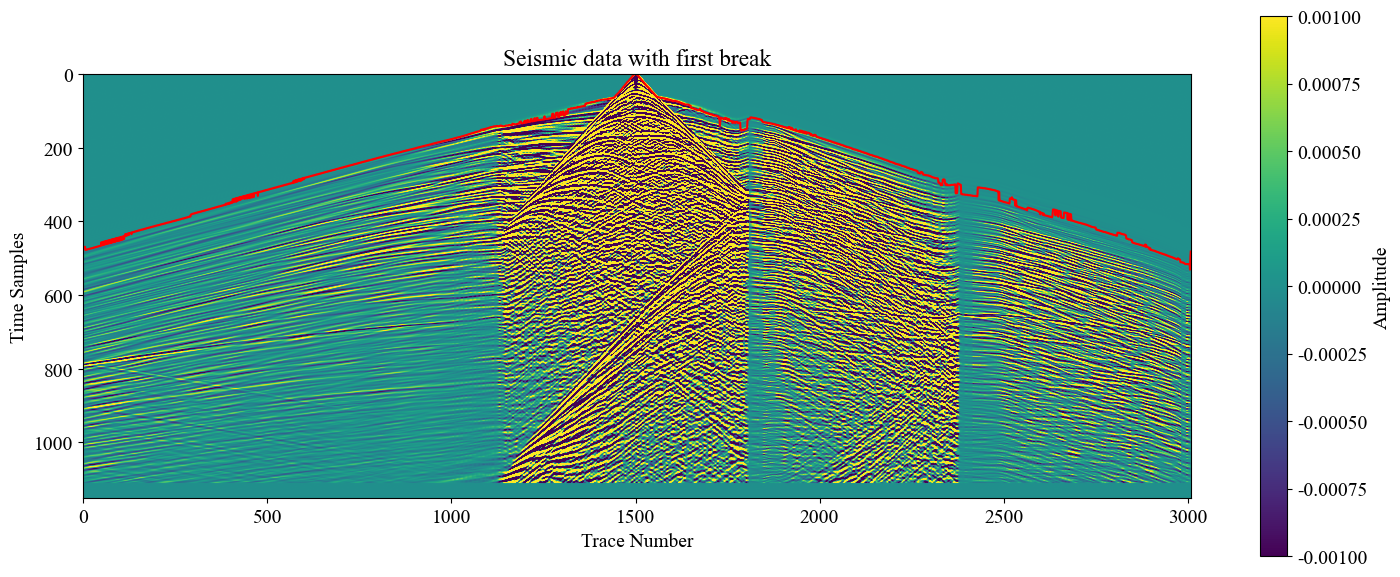
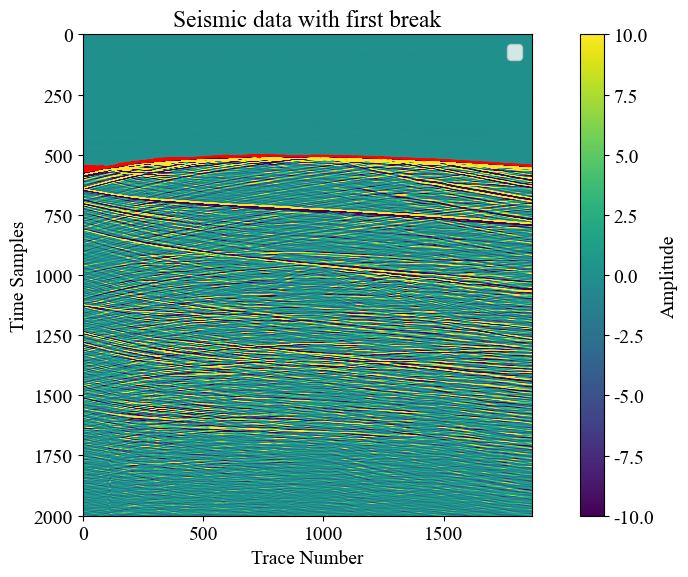
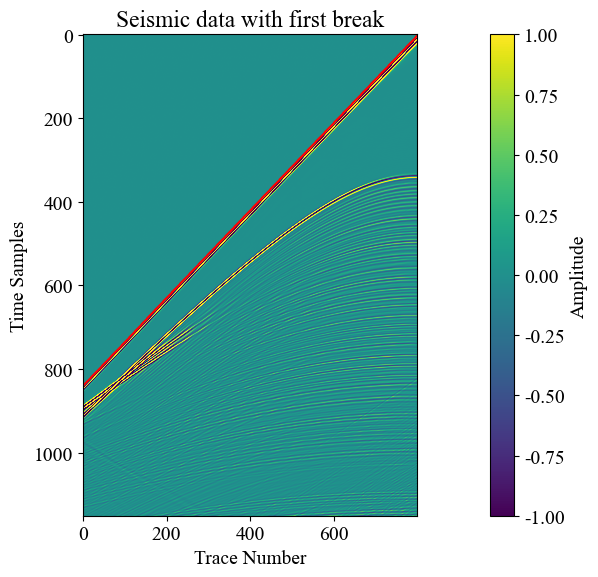
绘制地震单炮和计算出的初至，叠合显示，检查结果是否正确：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
plt.figure(figsize=(10, 6))  

# 绘制地震剖面
img = plt.imshow(model_vsp[0], aspect=1, vmin=-10, vmax=10)
plt.colorbar(label='Amplitude')

# 绘制初至
x = np.arange(model_vsp[0].shape[1])  
plt.plot(x,fb, 'r-', linewidth=1.5)

plt.xlabel('Trace Number')
plt.ylabel('Time Samples')
plt.title('Seismic data with first break')
plt.legend()

plt.tight_layout()
plt.show()

vsp_fb_checkover

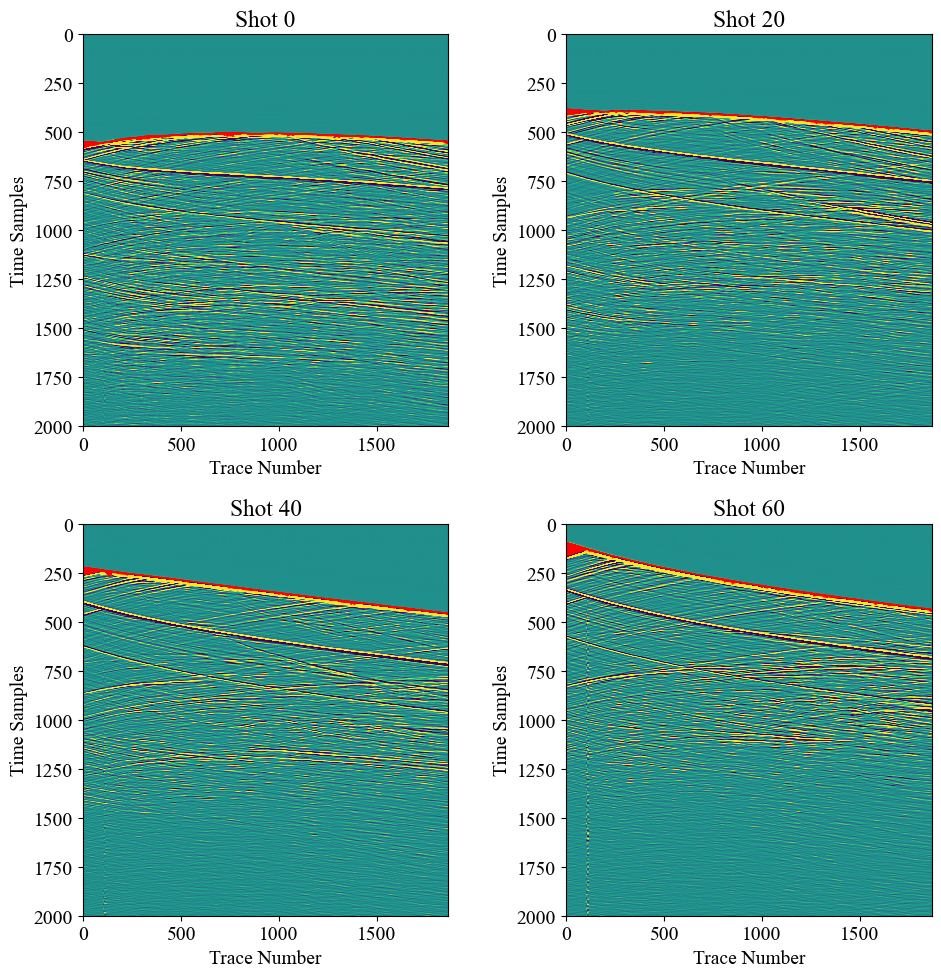
4. 计算所有炮的初至

1
2
3
4
5
6
7
8
shots, times, traces = model_vsp.shape
fb_all = np.zeros((shots, traces), dtype=int)

for i in range(shots):
    current_shot = model_vsp[i, :, :]
    fb_all[i, :] = calculate_fb(current_shot, threshold=0.05)

print(f"fb_all shape: {fb_all.shape}")

检查一下结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
fig, axes = plt.subplots(2, 2, figsize=(10, 10))
axes = axes.flatten()

model_vsp_list = [model_vsp[0], model_vsp[20], model_vsp[40], model_vsp[60]] 
fb_list = [fb_all[0], fb_all[20], fb_all[40], fb_all[60]] 
titles = ['Shot 0', 'Shot 20', 'Shot 40', 'Shot 60'] 

for i in range(4):
    img = axes[i].imshow(model_vsp_list[i], aspect=1, vmin=-10, vmax=10)
    x = np.arange(model_vsp_list[i].shape[1])
    axes[i].plot(x, fb_list[i], 'r-', linewidth=1.0)
    
    axes[i].set_xlabel('Trace Number')
    axes[i].set_ylabel('Time Samples')
    axes[i].set_title(f'{titles[i]}')

plt.tight_layout()
plt.show()

vsp_fb_all

The end

当然，本文只提供一种初至的近似解，如果数据质量好的话，初至当然比较完美，如果数据质量差的话，肯定也会有一些瑕疵。

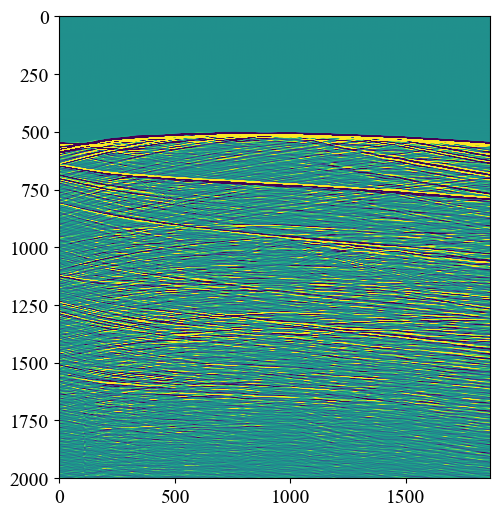
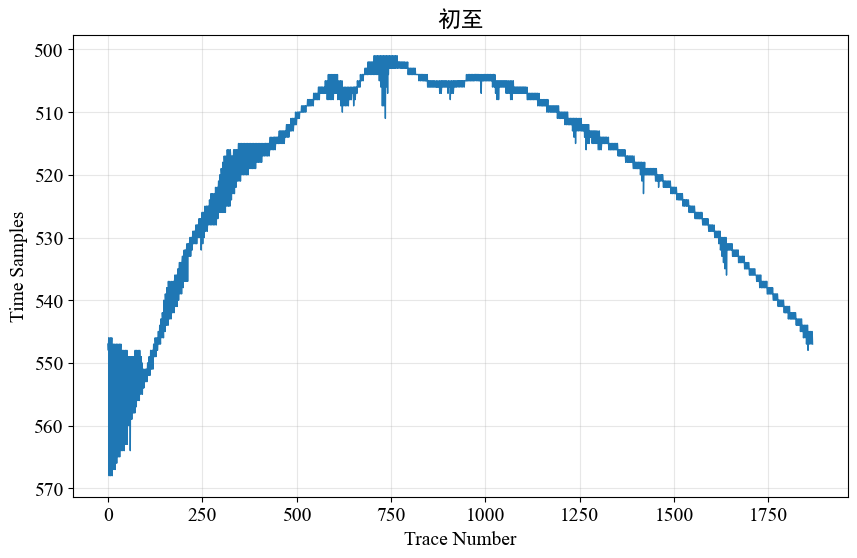
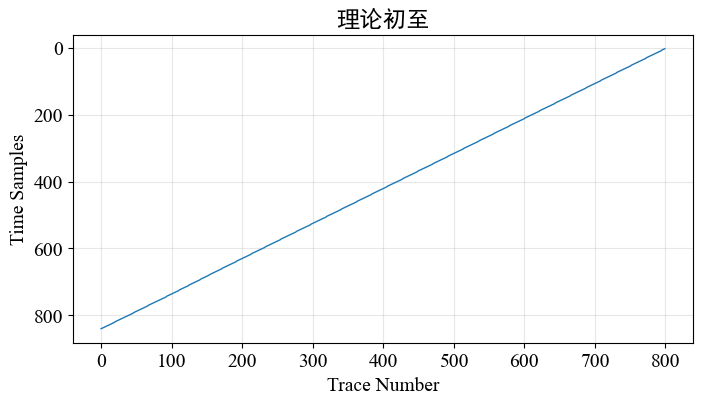
例如下面两组数据：数据来源：第一个数据model_ani, 第二个数据model_7m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
fb = calculate_fb(model_ani[0],threshold=0.01)   # model_7m[0]

plt.figure(figsize=(8, 4))
plt.plot(fb, linewidth=1)
plt.title('理论初至')
plt.xlabel('Trace Number')
plt.ylabel('Time Samples')
plt.gca().invert_yaxis()
plt.grid(True, alpha=0.3)
plt.show()

print(f"First Break shape = : {fb.shape}")
print(f"First Break range = : {np.min(fb)} - {np.max(fb)}")

#绘制地震单炮和初至的叠合显示
plt.figure(figsize=(15, 6))  
img = plt.imshow(model_ani[0,:,:], aspect=1, vmin=-0.001, vmax=0.001) 
plt.colorbar(label='Amplitude')

x = np.arange(model_ani[0].shape[1])  
plt.plot(x,fb, 'r-', linewidth=1.5)

plt.xlabel('Trace Number')
plt.ylabel('Time Samples')
plt.title('Seismic data with first break')

plt.tight_layout()
plt.show()

model_ani 初至计算结果：

model_ani
model_ani

model_7m 初至计算结果：

model_7m
model_7m