简述滤波器实现步骤

本例为一个简单的低通滤波器，具体步骤如下：

  1. 对雷克子波进行傅里叶变换，观察其在频率域的振幅谱图像。

  2. 在频率域设计低通滤波器，滤掉大于62.5Hz的高频成分。
    分别设计了理想低通滤波器和可以削弱Gibbs效应的加斜坡的滤波器（镶边法）。

  3. 绘制两种滤波器和滤波后信号的频率域振幅谱、时间域图像。

Matlab代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
function [] = Filtering()
clc;
clear;
close all;

m=100;                                    %采样点100
dt=0.002;                                 %时间采样间隔0.002
N=2^nextpow2(m);                          %取大于m最小的2的幂次
df=1/( N * dt );                          %空间间隔
%% 
[wavelet,~] = Ricker_zero(25,dt,m,3);     %中心频率25Hz，子波宽度r=3
wavelet(m+1:N) = 0;                       %补零

fft_wavelet=fft(wavelet);                 %对离散补零后子波进行快速傅氏变换
amplitude_wavelet=abs(fft_wavelet);       %振幅曲线

%% 设计低通滤波器,对频率为25Hz的信号进行滤波,滤掉大于62.5Hz频率成分
f = 62.5;
startFilter = f / df;
endFilter = N - startFilter;
%理想滤波器
for i = 1 : N
    value(i) = 1;
end
for i = startFilter + 1 : endFilter - 1
    value(i) = 0;
end
%加斜坡滤波器
for i = 1 : N
    value_slope(i)=1;
end
for i = (startFilter + 8) : (endFilter - 8)
    value_slope(i)=0;
end
for i = startFilter : startFilter + 8
    value_slope(i) = -1/8 * i + 1 + 1/8 * startFilter;
end
for i = endFilter - 8 : endFilter
    value_slope(i) = 1/8 * i + 1 -1/8 * endFilter;
end

%频率域滤波
for i = 1 : N
    freq_ideal(i) = value(i)*fft_wavelet(i);
    freq_slope(i) = value_slope(i)*fft_wavelet(i);
end
%反变换回时间域
ifft_wavelet_ideal=ifft(freq_ideal);
ifft_wavelet_slope=ifft(freq_slope);

%% 绘图
x=1:N;
figure,
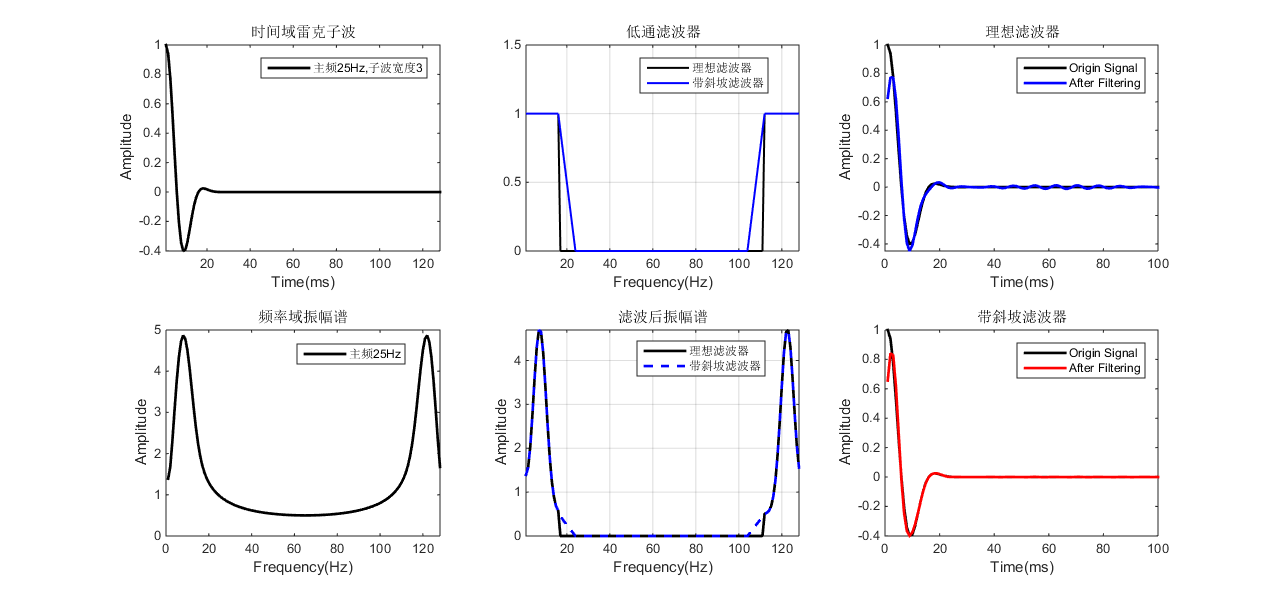
subplot(2,3,1)
plot(x,wavelet,'k','LineWidth',2.0)                    %绘制时间域子波
title('时间域雷克子波'),xlabel('Time(ms)'),ylabel('Amplitude'),axis([-inf inf -inf inf]),legend('主频25Hz,子波宽度3');

subplot(2,3,4)
plot(x,amplitude_wavelet,'k','LineWidth',2.0)          %绘制频率域振幅谱
title('频率域振幅谱'),xlabel('Frequency(Hz)'),ylabel('Amplitude'),legend('主频25Hz');
set(gca,'XLim',[0 N]);

subplot(2,3,2)
plot(x,value,'k',x,value_slope,'b','LineWidth',1.5)    %绘制滤波器
axis([-inf,inf,0,1.5]),title('低通滤波器'),xlabel('Frequency(Hz)'),legend('理想滤波器','带斜坡滤波器');
grid on
 
subplot(2,3,5)                                         %绘制滤波后振幅谱
plot(x,freq_ideal,'k',x,freq_slope,'b--','LineWidth',2.0)  
title('滤波后振幅谱'),xlabel('Frequency(Hz)'),ylabel('Amplitude'),legend('理想滤波器','带斜坡滤波器'),axis([-inf inf -inf inf])
grid on

subplot(2,3,3)                                         %绘制滤波后时间域信号
plot(x,wavelet,'k',x,real(ifft_wavelet_ideal),'b-','LineWidth',2.0)
title('理想滤波器'),legend('Origin Signal','After Filtering'),xlabel('Time(ms)'),ylabel('Amplitude'),axis([0 m -inf inf])
subplot(2,3,6)
plot(x,wavelet,'k',x,real(ifft_wavelet_slope),'r-','LineWidth',2.0)
title('带斜坡滤波器'),legend('Origin Signal','After Filtering'),xlabel('Time(ms)'),ylabel('Amplitude'),axis([0 m -inf inf])
end

function [wavelet_zero,time]=Ricker_zero(freqs,dt,nt,r)
% freqs:主频 
% dt:采样时间间隔
% nt:采样点数
% r: 子波宽度
tmin=0;
tmax=dt*nt;
time=tmin:dt:tmax;
wavelet_zero=exp(-(2*pi*freqs/r)^2*time.^2).*cos(2*pi*freqs.*time);
end

结果

Result

Reference

[1] 数字信号分析·课程作业