大地电磁二维正演公式中提到，求解二维大地电磁场的问题就是求解下式这样的偏微分方程的问题。

在开源程序FEMT2D中，Börner, R. U提供了二维亥姆霍兹偏微分方程的有限元解法。

1. FEMT2D程序如何获取

方式1：直接从Börner, R. U的Github仓库里下载。

方式2：利用Git克隆到本地：

1
git clone https://github.com/ruboerner/FEMT2D.git

下载好后，将得到下列文件：

2. FEMT2D如何使用

在FEMT2D程序的README.md文档中，已详细介绍了该程序的使用方法。本文以其中的一个例子作为演示。

第一步：

在运行FEMT2D程序之前，需要利用Triangle进行网格剖分.

该程序的网格剖分在python上进行，需安装PyGIMLi工具与Triangle程序。

Notice：在安装完成PyGIMLi环境后，需要将triangle.exe放在该环境的目录下。例如，我的PyGIMLi所在的文件夹为'D:\ProgramFiles\Anaconda3\envs\pg'，则应将'triangle.exe'也放在该文件夹中。

安装好这两样，下面的就很简单了。

第二步：

打开FEMT2D程序的Notebooks文件夹，该文件夹包含了所有Demo例子的网格剖分程序。

以第一个例子作为示范，打开’COMMEMI_2D_0.ipynb’（注意切换到PyGIMLi环境），运行该程序，便得到meshes文件夹下的四个网格文件。

1
2
3
4
5
meshes
├── commemi2d0.1.ele
├── commemi2d0.1.node
├── commemi2d0.1.poly
├── commemi2d0.poly

第三步：

打开matlab（切换路径至FEMT2D主文件夹），在命令行窗口运行

1
demo.driverCOMMEMI_2D_0

就ok了。

下面是该例子的运行结果：

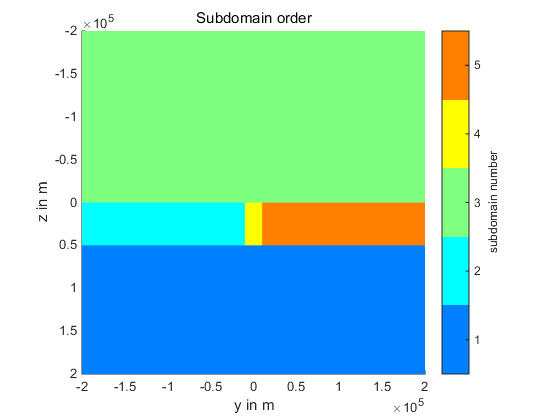
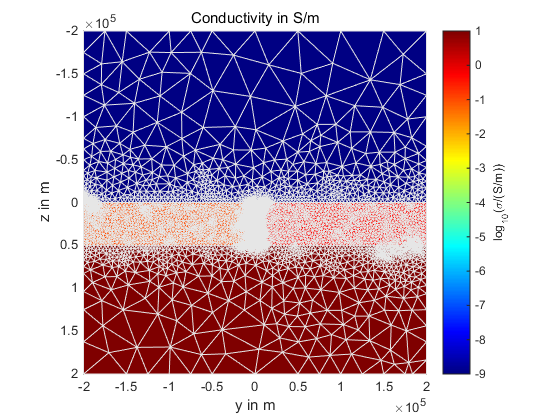
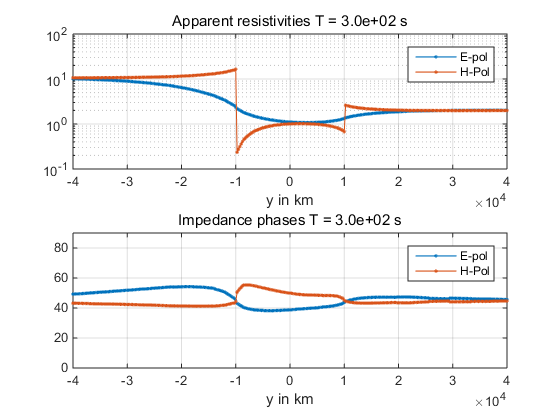
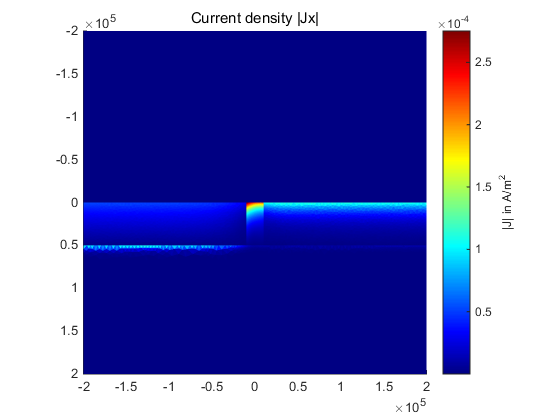
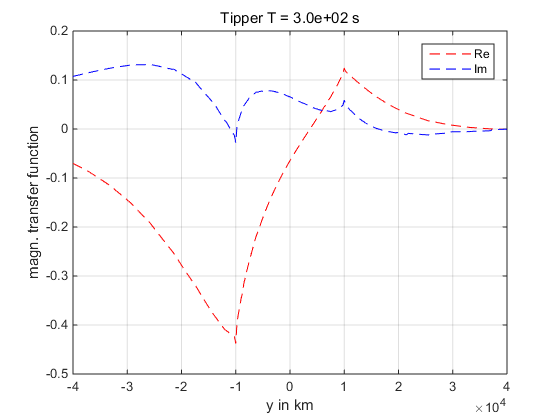
References

[1] Börner, R. U. 的Github repository - FEMT2D

[2] FEMT2D: FE simulation of 2D Magnetotellurics in MATLAB. https://doi.org/10.5281/zenodo.3955407

[3] Jonathan Richard Shewchuk, Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator, in “Applied Computational Geometry: Towards Geometric Engineering” (Ming C. Lin and Dinesh Manocha, editors), volume 1148 of Lecture Notes in Computer Science, pages 203-222, Springer-Verlag, Berlin, May 1996.

[4] Jonathan Richard Shewchuk, Delaunay Refinement Algorithms for Triangular Mesh Generation, Computational Geometry: Theory and Applications 22(1-3):21-74, May 2002.

[5] Franke, A., Börner, R. U., & Spitzer, K. (2007). Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography. Geophysical Journal International, 171(1), 71-86.

[6] Börner, R. U. (2010). Numerical modelling in geo-electromagnetics: advances and challenges. Surveys in Geophysics, 31(2), 225-245.

[7] Rücker, C., Günther, T., Wagner, F.M., 2017. pyGIMLi: An open-source library for modelling and inversion in geophysics, Computers and Geosciences, 109, 106-123, doi: 10.1016/j.cageo.2017.07.011.