大地电磁二维正演 | MT2D Forward 公式(各向同性)

下面介绍二维地电模型上的大地电磁场公式。首先，让我们回顾在大地电磁一维正演公式中，提到过的似稳态麦克斯韦方程组（文中式$(10),(11)$）。

回顾似稳态麦克斯韦方程组

假定时间因子为$e^{i\omega t}$，似稳态麦克斯韦方程为：

$$\nabla\times E=-i\omega u_0H \tag{10}$$ $$\nabla\times H=\sigma E \tag{11}$$

将式$(10)$展开得：

$$\begin{aligned} \nabla\times E &= \begin{vmatrix} \overrightarrow i &\overrightarrow j&\overrightarrow k\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ E_x&E_y&E_z\\ \end{vmatrix} \\& =(\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z})\overrightarrow i+ (\frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x})\overrightarrow j+ (\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y})\overrightarrow k \\& =-i\omega u_0(H_x\overrightarrow i+H_y\overrightarrow j+H_Z\overrightarrow k) \end{aligned} \tag{12}$$

将式$(11)$展开得：

$$\begin{aligned} \nabla\times H &= \begin{vmatrix} \overrightarrow i &\overrightarrow j&\overrightarrow k\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ H_x&H_y&H_z\\ \end{vmatrix} \\ &=(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z})\overrightarrow i+ (\frac{\partial H_x}{\partial z}-\frac{\partial H_z}{\partial x})\overrightarrow j+ (\frac{\partial H_y}{\partial x}-\frac{\partial H_x}{\partial y})\overrightarrow k \\& =\sigma (E_x\overrightarrow i+E_y\overrightarrow j+E_Z\overrightarrow k) \end{aligned} \tag{13}$$

二维地电模型的大地电磁场

考虑2D地电模型。假定电导率沿走向方向没有变化。取直角坐标系，设$x$轴平行走向方向，正$z$轴垂直向下指向大地。电导率沿走向方向没有变化意味着偏导数$\frac{\partial}{\partial x}$相对于$\frac{\partial}{\partial y},\frac{\partial}{\partial z}$可以省略不计，于是，方程$(10)$和$(11)$分解为两个相互独立的极化模式：

1.TE-模式(E-极化)

$$\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z} = \sigma E_x \tag{14}$$ $$\frac{\partial E_x}{\partial z} = -i\omega u_0H_y \tag{15}$$ $$\frac{\partial E_x}{\partial y} = i\omega u_0H_Z \tag{16}$$

由方程$(14)-(16)$，可以得到电场$E_x$分量所满足的偏微分方程：

$$\nabla^2E_x-i\omega u_0\sigma E_x = 0 \tag{17}$$

2.TM-模式(B-极化)

$$\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z} = -i\omega u_0H_x \tag{18}$$ $$\frac{\partial H_x}{\partial z} = \sigma E_y \tag{19}$$ $$-\frac{\partial H_x}{\partial y} = \sigma E_z \tag{20}$$

由方程$(18)-(20)$，可以得到磁场$H_x$分量所满足的偏微分方程：

$$\nabla^2H_x-i\omega u_0\sigma H_x = 0 \tag{21}$$

二维地电模型的TE和TM模式

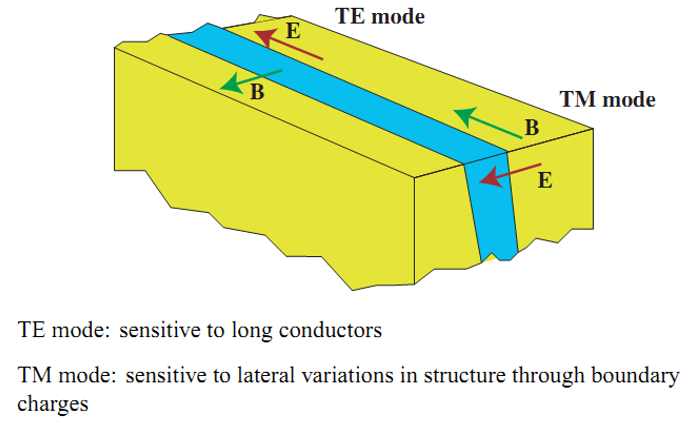
TE-模式(E-极化)描述了一个由与走向方向垂直的磁场所激发的沿走向方向的电场，而TM-模式(B-极化)描述了一个与走向方向平行的磁场所激发的与其垂直的电场。

二维模型大地电磁场

$$\nabla^2E_x-i\omega u_0\sigma E_x = 0 \tag{17}$$ $$\nabla^2H_x-i\omega u_0\sigma H_x = 0 \tag{21}$$

因此，求解二维大地电磁场的问题其实就是求解式$(17),(21)$这样的偏微分方程(组)的问题。

• 只有少数简单规则模型（如均匀半空间、一维层状模型、垂直界面、球体、圆柱体等）的电磁场边值问题存在解析解。

• 对于大多数模型，只能用数值方法解边值问题得到近似数值解。目前，在电磁场数值模拟中常用的数值方法有有限差分法、有限单元法、积分方程法、边界单元法等。

二维地电模型的视电阻率和相位

$$\rho_{xy} = \frac{1}{\omega u_0}|\frac{E_x}{H_y}|^2 {\quad\quad} \phi_{xy} = arg(\frac{E_x}{H_y})$$ $$\rho_{yx} = \frac{1}{\omega u_0}|\frac{E_y}{H_x}|^2 {\quad\quad} \phi_{yx} = arg(\frac{E_y}{H_x})$$

$ \rho{xy}, \phi{xy} $ (或$ \rho{TE}, \phi{TE} $)分别表示TE极化时的视电阻率和相位；

$ \rho{yx}, \phi{yx} $ (或$ \rho{TM}, \phi{TM} $)分别表示TM极化时的视电阻率和相位。

Reference:

[1] 李予国老师2021年海洋电磁学课程讲义