该模型是Alan Jones，2019中提到的一个Bakken模型，是对Strack，2014文献中的Bakken页岩层的简化。（即 Alan jones，2019文献中“EXAMPLE OF APPLICATION FOR AN “IMPOSSIBLE” PROBLEM”部分的例子。）

通过该例可以看到，含/不含高阻薄层的正演响应曲线十分接近，这也是MT反演时难以识别高阻薄层的原因。

高阻薄层-模型参数

该模型中，高阻薄层厚度为10 m，电阻率值为120 Ω·m，其上方是30 Ω·m的相对低阻层，下方是2.5 Ω·m的均匀半空间。下表列出了含有高阻薄层与不含高阻薄层的模型参数。

Bakken模型（含高阻薄层） without Bakken模型（不含高阻薄层）
深度(顶界面) (m) 电阻率值(Ω·m) 深度(顶界面) (m) 电阻率值(Ω·m)
0 30 0 30
155 120 155 30
165 2.5 165 2.5
Bakken model （含高阻薄层模型）
withoutBakken model （不含高阻薄层模型）

正演响应

下面绘制withBakken（含有高阻薄层）模型与withoutBakken（不含高阻薄层）模型的正演响应曲线：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
function ShowMT1DForward_withorwithoutBakken(varargin)
f = logspace(-3,3,21)';
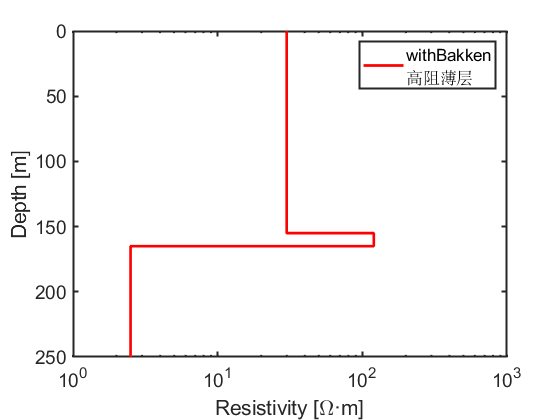
rho_withBakken = [30;120;2.5];        % 高阻薄层
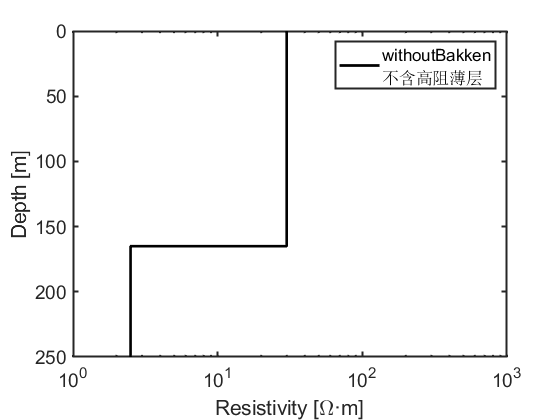
rho_withoutBakken = [30;30;2.5];      % 不含高阻薄层
h = [155;10];                         % 两个厚度(最后一层为均匀半空间)  

% 绘制含有高阻薄层的模型 
[x,y] = Getxy(rho_withBakken,h,85);
figure,       
semilogx(x,y,'-r','LineWidth',2.0);
axis([10^0,10^3,-inf,inf]);
set(gca,'YDir','rev','LineWidth',1.5,'FontSize',14);
xlabel('Resistivity [\Omega·m]');
ylabel('Depth [m]');
legend(['withBakken',newline,'高阻薄层']);

% 绘制不含高阻薄层的模型
[x1,y1] = Getxy(rho_withoutBakken,h,85);
figure,       
semilogx(x1,y1,'-k','LineWidth',2.0);
axis([10^0,10^3,-inf,inf]);
set(gca,'YDir','rev','LineWidth',1.5,'FontSize',14);
xlabel('Resistivity [\Omega·m]');
ylabel('Depth [m]');
legend(['withoutBakken',newline,'不含高阻薄层']);

% 调用正演函数，计算视电阻率和相位
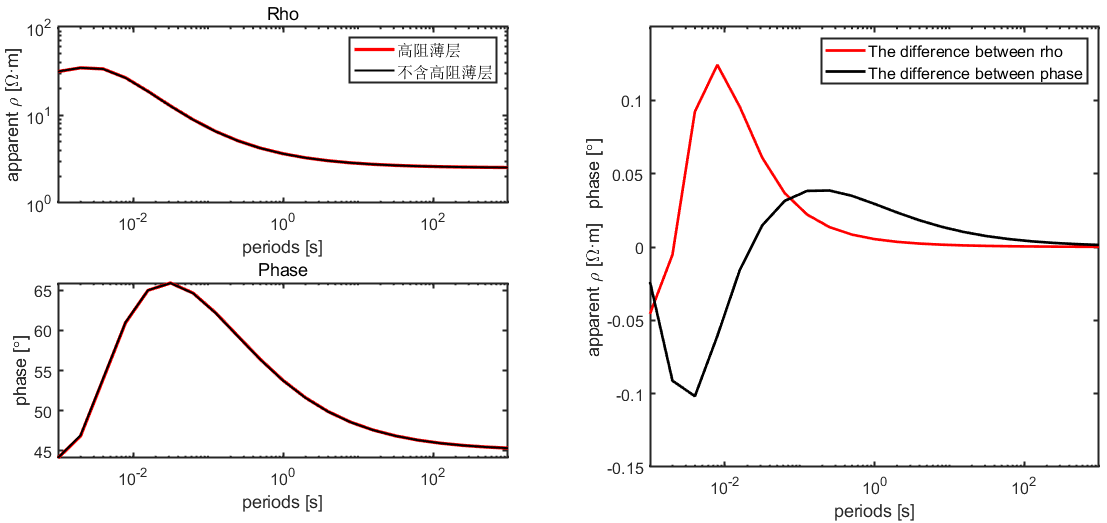
[apparentRho_1,Phase_1]=MT1DForward(rho_withBakken,h,f);
[apparentRho_2,Phase_2]=MT1DForward(rho_withoutBakken,h,f);

% 绘制正演响应结果
figure,
subplot(2,2,1)
    plot(1./f,apparentRho_1,'-r','LineWidth',2.5)
    hold on;
    plot(1./f,apparentRho_2,'-k','LineWidth',1.5)
    set(gca,'Yscale','log','Xscale','log','LineWidth',1.5,'FontSize',12)
    xlabel('periods [s]');
    ylabel('apparent \rho [\Omega·m]')
    title('Rho');
    axis([10^-3,10^3,10^0,10^2]);
    legend('高阻薄层','不含高阻薄层','FontSize',12);
subplot(2,2,3)
    plot(1./f,Phase_1,'-r','LineWidth',2.5)
    hold on;
    plot(1./f,Phase_2,'-k','LineWidth',1.5)
    set(gca,'Xscale','log','LineWidth',1.5,'FontSize',12)
    xlabel('periods [s]');
    ylabel('phase [\circ]');
    title('Phase');
    axis([10^-3,10^3,-inf,inf]);
subplot(2,2,[2,4])
    plot(1./f,apparentRho_1-apparentRho_2,'-r','LineWidth',2.0)
    hold on;
    plot(1./f,Phase_1-Phase_2,'-k','LineWidth',2.0)
    set(gca,'Xscale','log','LineWidth',1.5,'FontSize',12)
    axis([10^-3,10^3,-0.15,0.15]);
    xlabel('periods [s]');
    ylabel('apparent \rho [\Omega·m]   phase [\circ]');
    legend('The difference between rho','The difference between phase','FontSize',12);

set(gcf,'unit','normalized','position',[0.2,0.2,0.7,0.5]);
end

% ------- Plot the 1D layered model -----from HanBo---- %
    function [x,y] = Getxy(rho, h, deep)
    Depth(1) = 0;                    % Depth数组存储每层的顶面埋深
    y(1) = Depth(1);
    if length(rho)>=2
        for j=2:length(rho)
            Depth(j) = Depth(j-1)+h(j-1);
            y(2*j-2) = Depth(j);
            y(2*j-1) = Depth(j);
        end
        y(2*j) = y(2*j-1) + deep;        % 设置画图时底部半空间的最大显示深度
    else
        y(2) = 1000;                % 若为均匀半空间，则显示到1000m
    end

    for j=1:length(rho)
        x(2*j-1)=rho(j);
        x(2*j)=rho(j);
    end

    end

其中，MT1DForward函数即“大地电磁一维正演”中提到的正演函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function [apparentRho,Phase] = MT1DForward(rho,h,f)  
% Notes goes here: https://cocklebur0924.github.io/2022/03/25/MT1D_Forward/
nFreqs = length(f);
nLayer = length(rho);

for iFreq = 1:nFreqs
    omega = 2*pi*f(iFreq);
    mu = 4*pi*1e-7;

for j = nLayer:-1:1
    k = sqrt(1i*omega*mu/rho(j));
    Z0 = sqrt(1i*omega*mu*rho(j));
    if j==nLayer
        Z = Z0;
        continue;
    end
    R = (Z0-Z)/(Z0+Z);
    Q = exp(-2*k*h(j));
    Z = Z0*(1-R*Q)/(1+R*Q);
end
            Z(iFreq)=Z;
            apparentRho(iFreq) = (abs(Z(iFreq)).^2)./(omega*mu);
            Phase(iFreq) = atan2d(imag(Z(iFreq)),real(Z(iFreq))); 
            % Notice:公式里计算出的相位单位为弧度，这里为°是因为使用atan2d函数转换成了度
end  
end

Result

正演响应曲线对比

Reference

[1] Jones A G. Beyond chi-squared: Additional measures of the closeness of a model to data. ASEG Extended Abstracts, 2019(1): 1~6

[2] Strack, K. M. (2014), Future Directions of Electromagnetic Methods for Hydrocarbon Applications, Surveys in Geophysics, 35(1), 157-177.