本文为Jones, 2018 和Jones, 2019两篇文献（实际上为同一篇文献，只是2019再版时加了一个Bakken模型的例子）中，”THE PROBLEM” 和 “A SOLUTION”部分的Toy Example的matlab实现。

Toy Example

Figure 1: Toy data and lowest-order polynomial that fits the data using $\chi^2$ as the distance measure of the closeness of the model to the data

Matlab实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
%% A toy example of 13 data points
% author:yangwen
% reference:Jones A G. Beyond chi-squared: Additional measures of the closeness of a model to data. ASEG Extended Abstracts, 2019(1): 1-6
% 
clear;
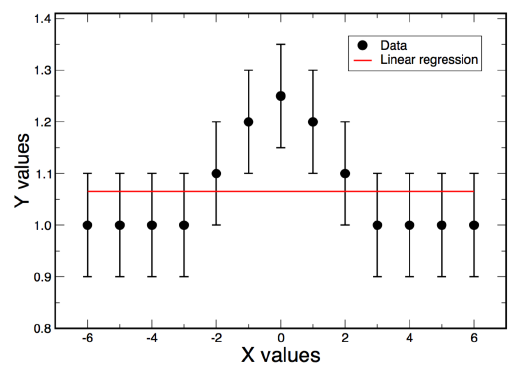
x = -6:1:6;
y = [1,1,1,1,1.1,1.2,1.25,1.2,1.1,1,1,1,1];
scatter(x,y,'filled','k','LineWidth',2);
axis([-7 7 0.8 1.4]);
% errorbar(x,y,0.1*ones(13,1),'k');

x1= -6:0.1:6;     %为了绘制光滑曲线，将x细分
hold on;
[p1,s1] = polyfit(x,y,1);
[y1,s1] = polyval(p1,x,s1);
plot(x1, polyval(p1, x1),'r','LineWidth',2);
% poly2str(p1)

hold on;
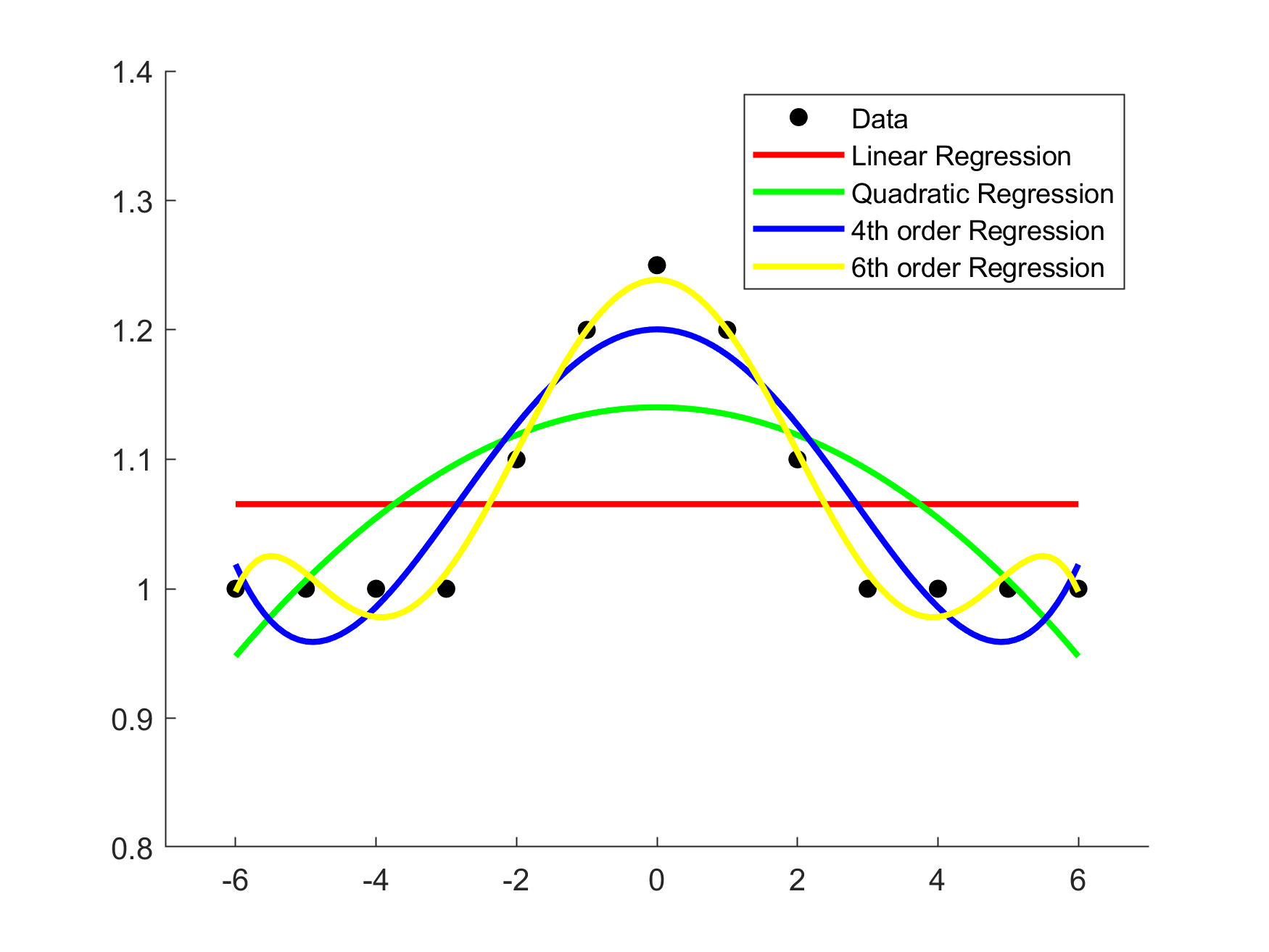
[p2,s2] = polyfit(x,y,2);
[y2,s2] = polyval(p2,x,s2);
plot(x1, polyval(p2, x1),'g','LineWidth',2);
% poly2str(p2)

hold on;
[p3,s3] = polyfit(x,y,4);
[y3,s3] = polyval(p3,x,s3);
plot(x1, polyval(p3, x1),'blue','LineWidth',2);
% poly2str(p3)

hold on;
[p4,s4] = polyfit(x,y,6);
[y4,s4] = polyval(p4,x,s4);
plot(x1, polyval(p4, x1),'y','LineWidth',2);
% poly2str(p4)
legend('Data','Linear Regression','Quadratic Regression','4th order Regression','6th order Regression');

%--------------------2021.4.11------------------------%
ans1 = 1.065;   % p1

ans2 = -0.0053447* x.^2 + 1.1402;        % p2

ans3 = 0.00041821* x.^4  - 0.020101* x.^2 + 1.2004;   % p3

ans4 = -2.924e-05* x.^6  + 0.0019998* x.^4  - 0.040793* x.^2  + 1.2387;  % p4

n = numel(x); %或者length(x)
% Misfit1 = sum(power(y-ans1,2)./power(s1,2));  %power(y-y1,2) = (y-y1).^2
Misfit1 = sum(power(y-ans1,2))*100;                 %Misfit1_ =sum((y-ans1).^2);
% RMS1 = sqrt(Misfit1/(n));
RMS1_ = sqrt(Misfit1/(n-1));

% Misfit2 = sum(power(y-ans2,2)./power(s2,2));
Misfit2 = sum(power(y-ans2,2)*100);
% RMS2 = sqrt(Misfit2/(n));
RMS2_ = sqrt(Misfit2/(n-1));

% Misfit3 = sum(power(y-ans3,2)./power(s3,2));
Misfit3 = sum(power(y-ans3,2))*100;
% RMS3 = sqrt(Misfit3/(n));
RMS3_ = sqrt(Misfit3/(n-1));

% Misfit4 = sum(power(y-ans4,2)./power(s4,2));
Misfit4 = sum(power(y-ans4,2))*100;
% RMS4 = sqrt(Misfit4/(n));
RMS4_ = sqrt(Misfit4/(n-1));
%--------------------------------------------%
%% compute dataMisfit and reduced nRMS
n = numel(x); %或者length(x)
% dataMisfit1 = sum(power(y-y1,2)./power(s1,2));  %power(y-y1,2) = (y-y1).^2
dataMisfit1 = sum(power(y-y1,2));
nRMS1 = sqrt(dataMisfit1/(n-1));

dataMisfit2 = sum(power(y-y2,2)./power(s2,2));
nRMS2 = sqrt(dataMisfit2/(n-1));

dataMisfit3 = sum(power(y-y3,2)./power(s3,2));
nRMS3 = sqrt(dataMisfit3/(n-1));

dataMisfit4 = sum(power(y-y4,2)./power(s4,2));
nRMS4 = sqrt(dataMisfit4/(n-1));

%% compute DW
%%
             e1=y1 - y;
             e1_=mean(e1);
            for ie=2:length(e1)
                dw_tem1(ie-1)=(e1(ie)-e1(ie-1))^2;
            end
            for ie=1:length(e1)
                dw_tem2(ie)=(e1(ie)-e1_)^2;
            end
             dw_1=sum(dw_tem1)/sum(dw_tem2);
%%
             e2=y2 - y;
             e2_=mean(e2);
            for ie=2:length(e2)
                dw_tem1(ie-1)=(e2(ie)-e2(ie-1))^2;
            end
            for ie=1:length(e2)
                dw_tem2(ie)=(e2(ie)-e2_)^2;
            end
             dw_2=sum(dw_tem1)/sum(dw_tem2);
%%
             e3=y3 - y;
             e3_=mean(e3);
            for ie=2:length(e3)
                dw_tem1(ie-1)=(e3(ie)-e3(ie-1))^2;
            end
            for ie=1:length(e3)
                dw_tem2(ie)=(e3(ie)-e3_)^2;
            end
             dw_3=sum(dw_tem1)/sum(dw_tem2);
%%
             e4=y4 - y;
             e4_=mean(e4);
            for ie=2:length(e4)
                dw_tem1(ie-1)=(e4(ie)-e4(ie-1))^2;
            end
            for ie=1:length(e4)
                dw_tem2(ie)=(e4(ie)-e4_)^2;
            end
             dw_4=sum(dw_tem1)/sum(dw_tem2);

Result：

最后得到Figure2的结果：

Figure 2: Toy data and polynomial fits to 6th order of the data

以及对应的参数（可能由于误差，有几个数据与原文献中Table1中的数值略有不同）。

Order Equations Data Misfit RMS DW statistic
0 $y= 1.0654$ 10.69 0.94 0.4209
2 $y= 1.1402 - 0.0053447 x^2$ 4.97 0.64 0.8679
4 $y= 1.2004- 0.020101 x^2+ 0.00041821 x^4 $ 1.47 0.35 1.7019
6 $y= 1.2387 - 0.040793 x^2 + 0.0019998 x^4- 2. 924 e-05 x^6$ 0.17 0.12 3.1084

Reference:

[1] Jones A G. Beyond chi-squared: Additional measures of the closeness of a model to data. SEG International Exposition and 88th annual Meeting, 2018, 1888~1892

[2] Jones A G. Beyond chi-squared: Additional measures of the closeness of a model to data. ASEG Extended Abstracts, 2019(1): 1~6