本系列为大地电磁一维反演的一些matlab程序，搬运自Mohammad Rheza Zamani的Github项目：1D-Magnetotelluric-Inversion ，共包括以下五种算法：

1D-Magnetotelluric-Inversion

  1. MT FA：萤火虫算法(Firefly Algorithm，FA)
  2. MT BA：蝙蝠算法(Bat algorithm，BA)
  3. MT PSO：粒子群优化算法(Particle Swarm Optimization，PSO)
  4. MT SA：模拟退火算法(Simulated Anealling，SA)
  5. MT VFSA：非常快速模拟退火算法(Very Fast Simulated Annealing，VFSA)

本节为模拟退火算法 MT1D Inversion matlab代码

模拟退火算法(SA)简介

模拟退火算法(Simulated Annealing，SA)是基于 Monte-Carlo 迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。该算法最早的思想是由N. Metropolis. et al.于1953年提出。1983年,S. Kirkpatrick等成功地将退火思想引入到组合优化领域$^{[1]}$。

模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解处能概率性地跳出并最终趋于全局最优。这里的“一定的概率”的计算参考了金属冶炼的退火过程，这也是模拟退火算法名称的由来$^{[1]}$。

SA 大地电磁一维反演matlab代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
%Program pemodelan inversi kurva sounding MT 1-D dengan
%menggunakan algoritma Simulated Anealling
%Mohammad Rheza Zamani
tic
clear all;
clc;
%Data sintetik
R = [100 1000 10];
thk = [500 1500];
freq = logspace(-3,3,50);
T = 1./freq;
[app_sin, phase_sin] = modelMT(R, thk ,T);

%Definisi ruang model 
nlayer = 3; %Jumlah lapisan 
nitr = 300; %Jumlah iterasi 
%Ruang pencarian diatur sebesar 5 kali dari model data  sintetik
%Batas bawah pencarian nilai resistivitas
LBR = [1 1 1];
%Batas atas pencarian nilai resistivitas
UBR = [200 2000 20];
%Batas bawah pencarian nilai ketebalan
LBT = [1 1];
%Batas atas pencarian nilai resistivitas
UBT = [1000 3000];
Temp = 5;
dec = 0.05;
%Membuat model awal acak
rho1(1 , :) = LBR + rand*(UBR - LBR);
thick1(1, :) = LBT + rand*(UBT - LBT);
%Menghitung misfit, apparent resistivity, dan phase model awal
[apparentResistivity1, phase1]=modelMT(rho1(1,:),thick1(1,:),T);
app_mod1(1,:)=apparentResistivity1;
phase_mod1(1,:)=phase1;
     
[misfit1]=misfitMT(app_sin,phase_sin,app_mod1(1,:),phase_mod1(1,:));
E1=misfit1;
for itr = 1 : nitr
    rho2(1 , :) = LBR + rand*(UBR - LBR);
    thick2(1, :) = LBT + rand*(UBT - LBT);
    [apparentResistivity2, phase2]=modelMT(rho2(1,:),thick2(1,:),T);
    app_mod2(1,:)=apparentResistivity2;
    phase_mod2(1,:)=phase2;
    [misfit2]=misfitMT(app_sin,phase_sin,app_mod2(1,:),phase_mod2(1,:));
    E2=misfit2;
    delta_E = E2 -E1;
    
    if delta_E < 0
        rho1 = rho2;
        thick1 = thick2;
         E1 = E2;
    else
        P = exp((-delta_E)/Temp);
        if  P >= rand
           rho1 = rho2;
           thick1 = thick2;
           E1 = E2;
        end
    end
    [apparentResistivity_new, phase_new]=modelMT(rho1(1,:),thick1(1,:),T);
    Egen(itr)=E1;
    Temp = Temp*(1-dec);
    Temperature(itr) = Temp;

    %Persiapan Ploting
    rho_plot = [0 R];
    thk_plot = [0 cumsum(thk) max(thk)*10000];
    rhomod_plot = [0 rho1];
    thkmod_plot = [0 cumsum(thick1) max(thick1)*10000];
    
end
toc
    %Plotting
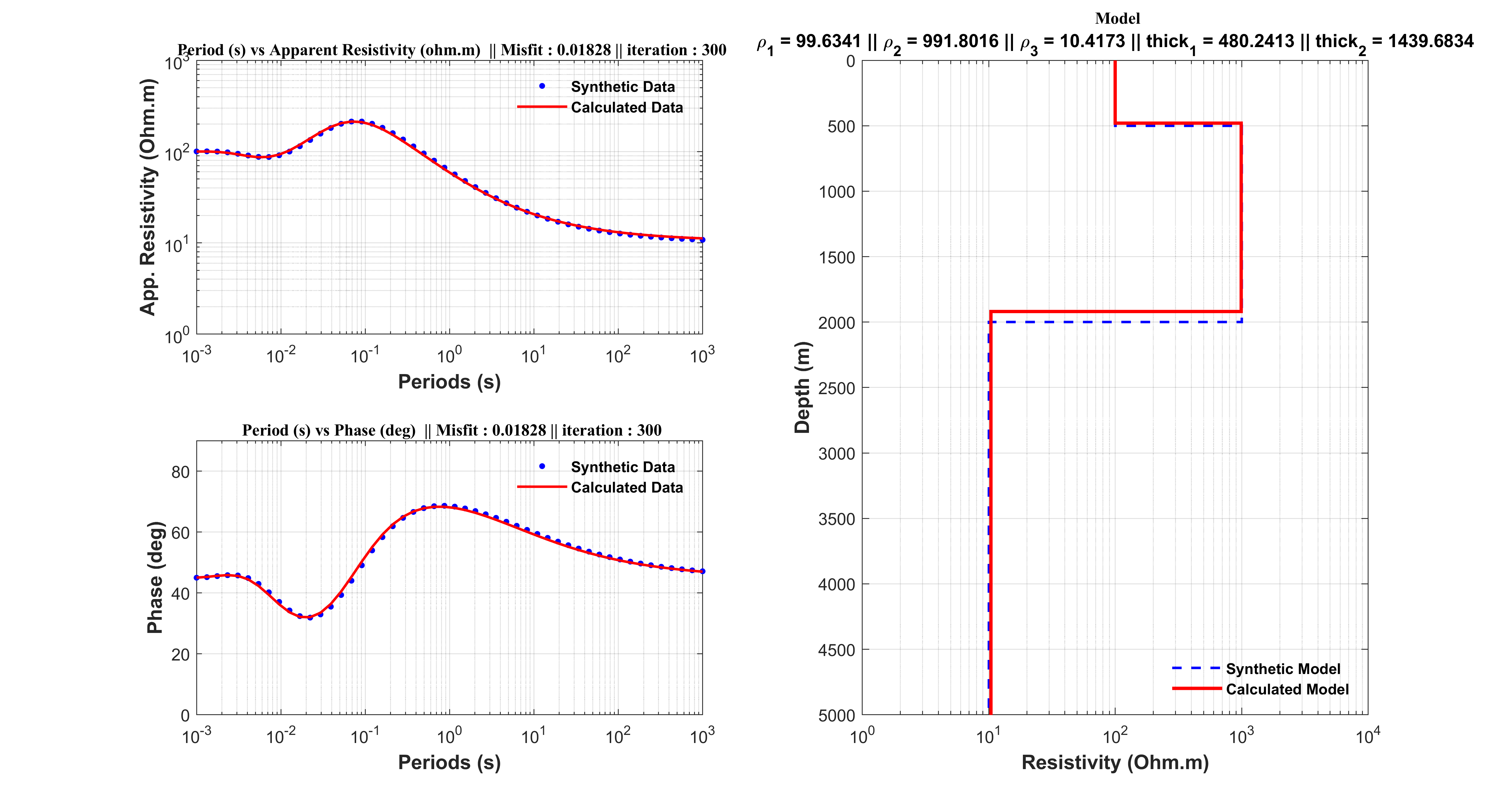
    figure(1)
    subplot(2, 2, 1)
    loglog(T,app_sin,'.b',T,apparentResistivity_new,'r','MarkerSize',12,'LineWidth',1.5);
    axis([10^-3 10^3 1 10^3]);
    legend({'Synthetic Data','Calculated Data'},'EdgeColor','none','Color','none','FontWeight','Bold');
    xlabel('Periods (s)','FontSize',12,'FontWeight','Bold');
    ylabel('App. Resistivity (Ohm.m)','FontSize',12,'FontWeight','Bold');
    title(['\bf \fontsize{10}\fontname{Times}Period (s) vs Apparent Resistivity (ohm.m)  || Misfit : ', num2str(Egen(itr)),' || iteration : ', num2str(itr)]);
    grid on
    
    subplot(2, 2, 3)
    loglog(T,phase_sin,'.b',T,phase_new,'r','MarkerSize',12,'LineWidth',1.5);
    axis([10^-3 10^3 0 90]);
    set(gca, 'YScale', 'linear');
    legend({'Synthetic Data','Calculated Data'},'EdgeColor','none','Color','none','FontWeight','Bold');
    xlabel('Periods (s)','FontSize',12,'FontWeight','Bold');
    ylabel('Phase (deg)','FontSize',12,'FontWeight','Bold');
    title(['\bf \fontsize{10}\fontname{Times}Period (s) vs Phase (deg)  || Misfit : ', num2str(Egen(itr)),' || iteration : ', num2str(itr)]);
    grid on
    
    subplot(2, 2, [2 4])
    stairs(rho_plot,thk_plot,'--b','Linewidth',1.5);
    hold on
    stairs(rhomod_plot ,thkmod_plot,'-r','Linewidth',2);
    hold off
     legend({'Synthetic Model','Calculated Model'},'EdgeColor','none','Color','none','FontWeight','Bold','Location','SouthEast');
    axis([1 10^4 0 5000]);
    xlabel('Resistivity (Ohm.m)','FontSize',12,'FontWeight','Bold');
    ylabel('Depth (m)','FontSize',12,'FontWeight','Bold');
    title(['\bf \fontsize{10}\fontname{Times}Model']);
    subtitle(['\rho_{1} = ',num2str(rho1(1)),' || \rho_{2} = ',num2str(rho1(2)),' || \rho_{3} = ',num2str(rho1(3)),' || thick_{1} = ',num2str(thick1(1)),' || thick_{2} = ',num2str(thick1(2))],'FontWeight','bold')
    set(gca,'YDir','Reverse');
    set(gca, 'XScale', 'log');
    set(gcf, 'Position', get(0, 'Screensize'));
    grid on

    %plot misfit
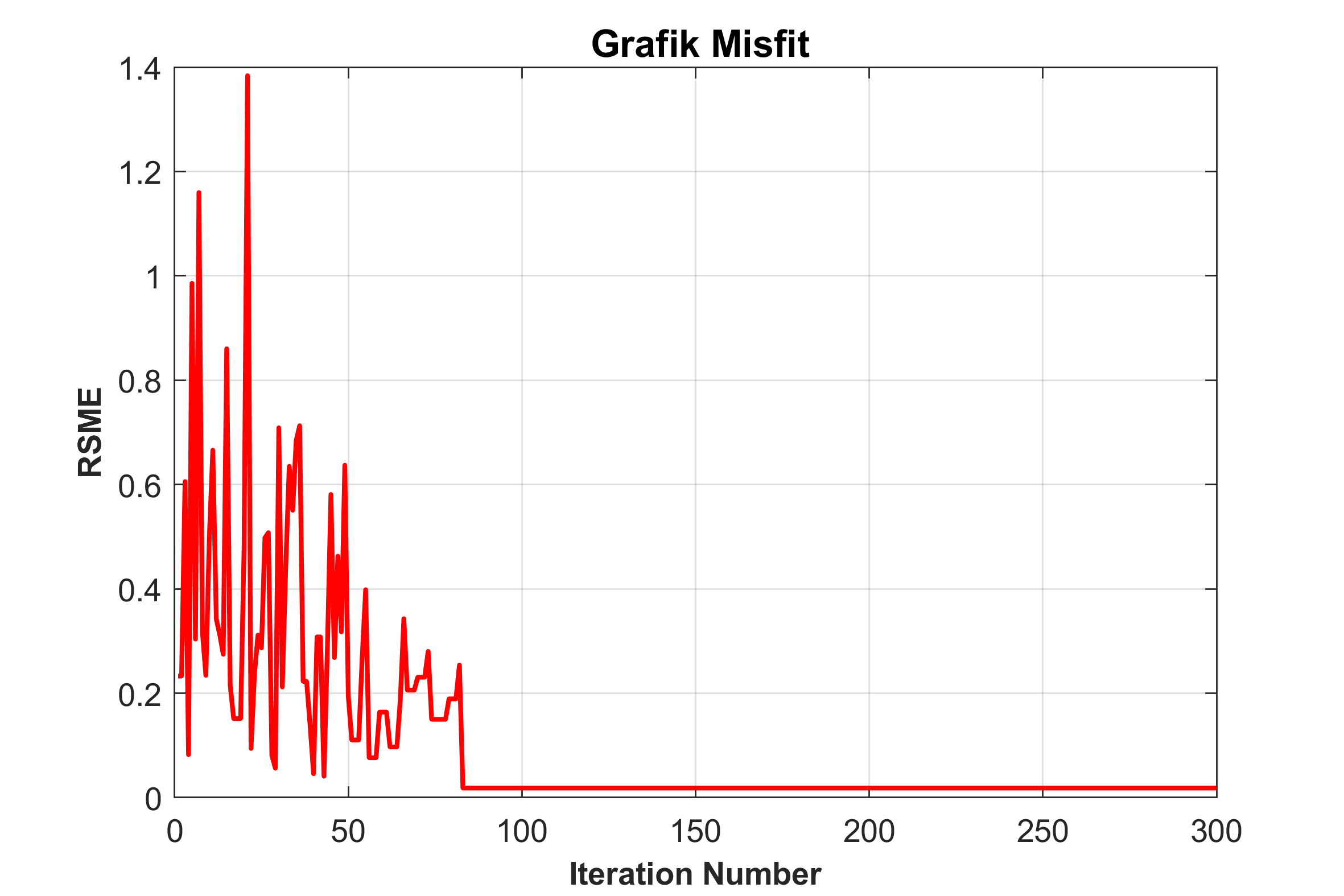
    figure(2)
    plot(1:nitr,Egen,'r','Linewidth',1.5)
    xlabel('Iteration Number','FontSize',10,'FontWeight','Bold');
    ylabel('RSME','FontSize',10,'FontWeight','Bold');
    title('\bf \fontsize{12} Grafik Misfit ');
    set(gcf, 'Position', get(0, 'Screensize'));
    grid on

    %Plot Temperature
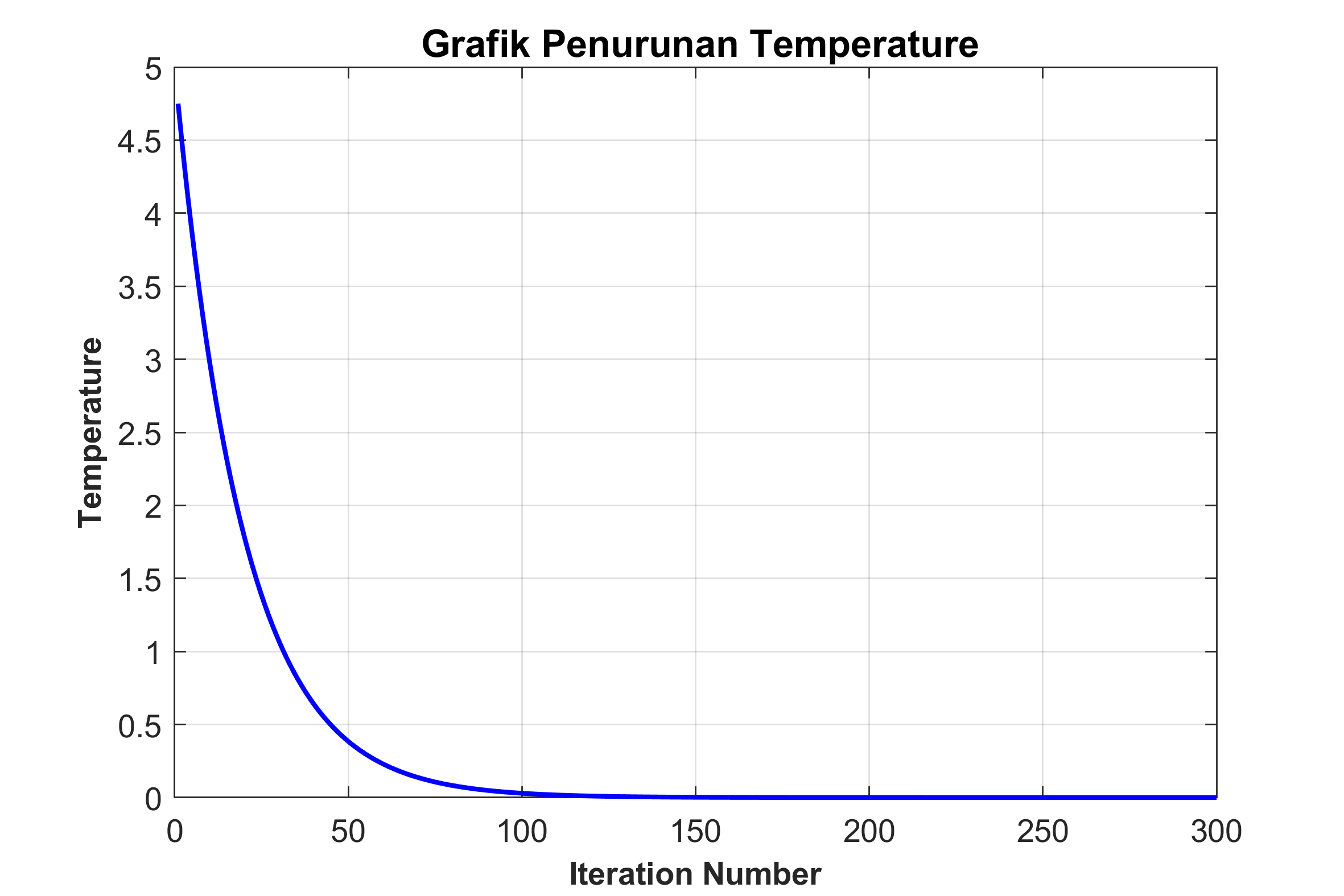
    figure(3)
    plot(1:nitr,Temperature,'b','Linewidth',1.5)
    xlabel('Iteration Number','FontSize',10,'FontWeight','Bold');
    ylabel('Temperature','FontSize',10,'FontWeight','Bold');
    title('\bf \fontsize{12} Grafik Penurunan Temperature ');
    set(gcf, 'Position', get(0, 'Screensize'));
    grid on

其中，子函数modelMT与misfitMT与萤火虫算法一致。

SA 反演结果

左:反演模型响应对比；右:反演结果对比
SA反演过程中RMSE变化曲线
SA反演过程中Temperature变化曲线

The end

Reference

[1] 知乎回答：模拟退火算法详解

[2] Mohammad Rheza Zamani的Github项目:1D-Magnetotelluric-Inversion之模拟退火算法