Firefly Algorithm(FA)大地电磁一维反演 | 萤火虫算法

本系列为大地电磁一维反演的一些matlab程序，搬运自Mohammad Rheza Zamani的Github项目：1D-Magnetotelluric-Inversion ，共包括以下五种算法：

1D-Magnetotelluric-Inversion

1. MT FA：萤火虫算法(Firefly Algorithm，FA)
2. MT BA：蝙蝠算法(Bat algorithm，BA)
3. MT PSO：粒子群优化算法(Particle Swarm Optimization，PSO)
4. MT SA：模拟退火算法(Simulated Anealling，SA)
5. MT VFSA：非常快速模拟退火算法(Very Fast Simulated Annealing，VFSA)

本节为萤火虫算法 MT1D Inversion matlab代码

萤火虫算法(FA)简介

萤火虫算法(Firefly Algorithm，简称FA)是一种模拟萤火虫闪烁行为的群体智能优化算法，由剑桥大学Xin-She Yang教授于2009年提出$^{[1]}$。

萤火虫之间通过闪光进行信息的交互，同时也能起到危险预警的作用。我们知道，从光源到特定距离$r$处的光强服从平方反比定律，也就是说，光强$I$随着距离$r$的增加会逐渐降低，即$I\propto 1/r^2$，此外空气也会吸收部分光线，导致光线随着距离的增加而变得越来越弱。这两个因素同时起作用，因而大多数萤火虫只能在有限的距离内被其他萤火虫发现$^{[1,2]}$。

为了方便算法的描述，作者给出了三个理想化的假设：

1. 所有萤火虫雌雄同体，以保证不管萤火虫性别如何，都能被其他萤火虫所吸引；

2. 吸引度与它们的亮度成正比，因此，对于任何两只闪烁的萤火虫，较暗的那只会朝着较亮的那只移动。吸引力与亮度程度会随着距离的增加而减小。最亮的萤火虫会随机选择方向进行移动。

3. 萤火虫的亮度可受目标函数影响或决定，对于最大化问题，亮度可以简单地与目标函数值成正比。

基于这三条假设，Firefly Algorithm(FA)可以被总结为图一所示的伪代码$^{[1]}$：

萤火虫算法伪代码(Yang XS, 2009 Fig.1)

FA 大地电磁一维反演 matlab 代码

%Program pemodelan inversi kurva sounding MT 1-D dengan
%menggunakan algoritma FA (Firefly Algorithm)
%Mohammad Rheza Zamani
tic
clear all;
clc;
%Data sintetik
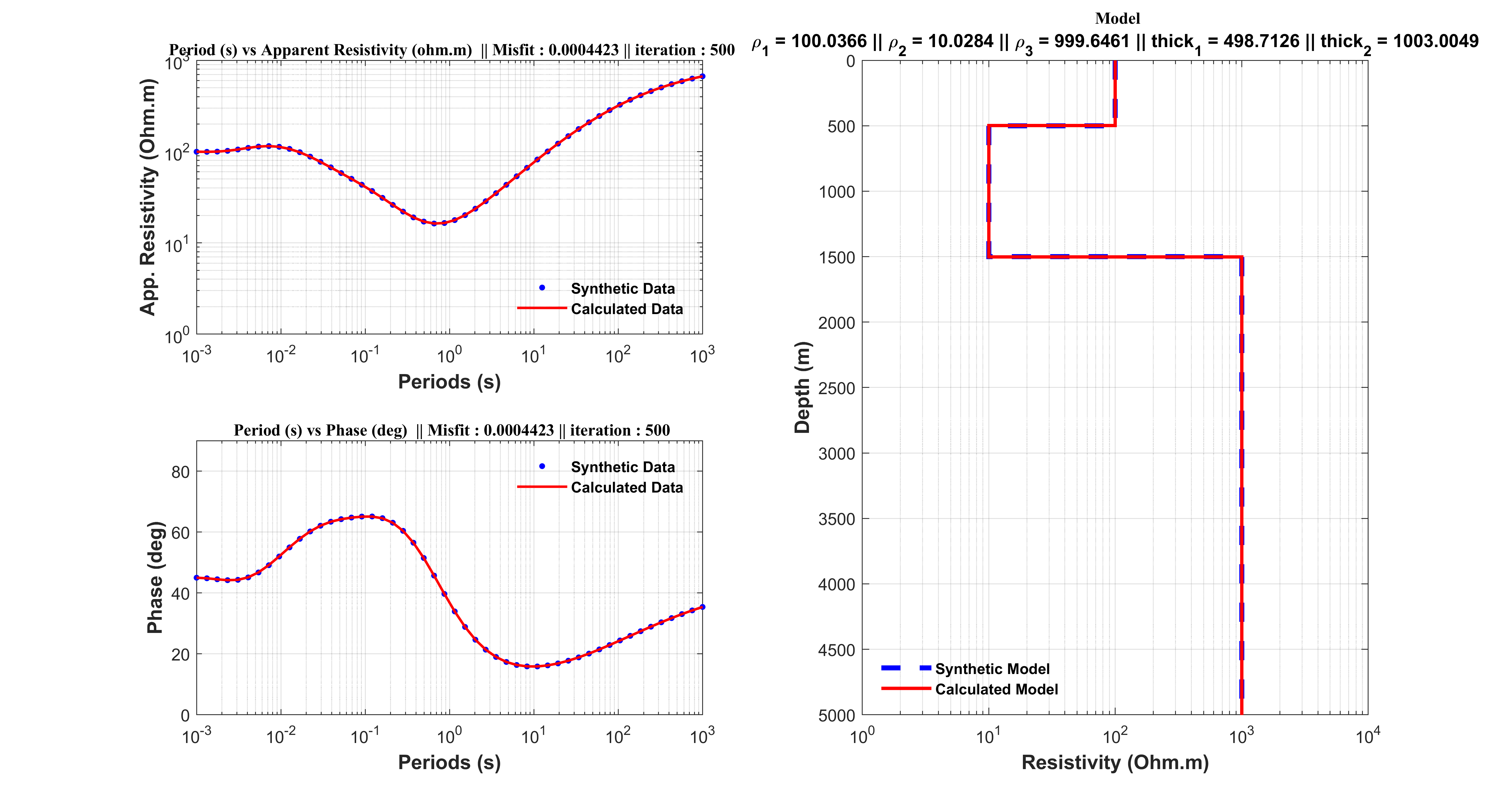
R = [100 10 1000];
thk = [500 1000];
freq = logspace(-3,3,50);
T = 1./freq;
[app_sin, phase_sin] = modelMT(R, thk ,T);

%Definisi ruang model 
npop = 100; %Jumlah dari model  
nlayer = 3; %Jumlah lapisan 
nitr = 500; %Jumlah iterasi 
%Ruang pencarian diatur sebesar 5 kali dari model data  sintetik
%Batas bawah pencarian nilai resistivitas
LBR = [1 1 1];
%Batas atas pencarian nilai resistivitas
UBR = [500 50 5000];
%Batas bawah pencarian nilai ketebalan
LBT = [1 1];
%Batas atas pencarian nilai resistivitas
UBT = [2500 5000];
alpha = 0.2;
betha0 = 1;
gamma = 0.8;
damp = 0.99;
%Membuat model awal
%Membuat model awal acak
for ipop = 1 : npop
    rho(ipop , :) = LBR + rand*(UBR - LBR);
    thick(ipop, :) = LBT + rand*(UBT - LBT);
end

for ipop=1:npop
    [apparentResistivity, phase_baru]=modelMT(rho(ipop,:),thick(ipop,:),T);
     app_mod(ipop,:)=apparentResistivity;
     phase_mod(ipop,:)=phase_baru;
     
    [misfit]=misfitMT(app_sin,phase_sin,app_mod(ipop,:),phase_mod(ipop,:));
    E(ipop)=misfit;
end
%Inversi
for itr = 1 : nitr
    for i =  1 : npop
        j = randi(npop,1);
        while i == j
            j = randi(npop,1);
        end
        if E(i)<E(j)
            %Calculated Distance
            dr = norm((rho(i,:)-rho(j,:)));
            dt = norm((thick(i,:)-thick(j,:)));
            %Calculated new model with determine a new position
            %Random vector position for resistivity model
            for n1 = 1 : nlayer
                rho_baru(1,n1) = rho(i,n1) +betha0.*exp(-gamma*(dr)^2).*(rho(j,n1)-rho(i,n1))+ (alpha*(rand-0.5)*abs((UBR(n1)-LBR(n1))));
                if rho_baru(1,n1) < LBR(n1);
                     rho_baru(1,n1) = LBR(n1);
                end
                if rho_baru(1,n1) > UBR(n1);
                     rho_baru(1,n1) = UBR(n1);
                end
            end
            %Random vector position for thick model
            for n2 = 1 : (nlayer-1)
                thk_baru(1,n2) = thick(i,n2) +betha0.*exp(-gamma*(dt)^2).*(thick(j,n2)-thick(i,n2))+ (alpha*(rand-0.5)*abs((UBT(n2)-LBT(n2))));
                if thk_baru(1,n2) < LBT(n2);
                     thk_baru(1,n2) = LBT(n2);
                end
                if thk_baru(1,n2) > UBT(n2);
                    thk_baru(1,n2) = UBT(n2);
                end
            end 
        else
            rho_baru(1,:) = rho(i,:);
            thk_baru(1,:) = thick(i,:);
        end
        [apparentResistivity_baru, phase_baru]=modelMT(rho_baru,thk_baru,T);
        [err] = misfitMT(app_sin,phase_sin,apparentResistivity_baru, phase_baru);
        %Update model dan error jika lebih baik
        if err<E(i)
            rho(i,:) = rho_baru(1,:);
            thick(i,:) = thk_baru(1,:);
            app_mod(i,:) = apparentResistivity_baru(1,:);
            phase_mod(i,:) = phase_baru(1,:);
            E(i) = err;
        end
      
    end
     Emin = 100;
        for ipop = 1 : npop
        if E(ipop)< Emin
            Emin = E(ipop);
            rho_model = rho(ipop,:);
            thk_model = thick(ipop,:);
            app_model = app_mod(ipop,:);
            phase_model = phase_mod(ipop,:);
        end
    end
    Egen(itr)=Emin;
    alpha = alpha*damp;
end
time = toc

    %Persiapan Ploting
    rho_plot = [0 R];
    thk_plot = [0 cumsum(thk) max(thk)*10000];
    rhomod_plot = [0 rho_model];
    thkmod_plot = [0 cumsum(thk_model) max(thk_model)*10000];
    %Plotting
    figure(1)
    subplot(2, 2, 1)
    loglog(T,app_sin,'.b',T,app_model,'r','MarkerSize',12,'LineWidth',1.5);
    axis([10^-3 10^3 1 10^3]);
    legend({'Synthetic Data','Calculated Data'},'EdgeColor','none','Color','none','FontWeight','Bold','location','southeast');
    xlabel('Periods (s)','FontSize',12,'FontWeight','Bold');
    ylabel('App. Resistivity (Ohm.m)','FontSize',12,'FontWeight','Bold');
    title(['\bf \fontsize{10}\fontname{Times}Period (s) vs Apparent Resistivity (ohm.m)  || Misfit : ', num2str(Egen(itr)),' || iteration : ', num2str(itr)]);
    grid on
    
    subplot(2, 2, 3)
    loglog(T,phase_sin,'.b',T,phase_model,'r','MarkerSize',12,'LineWidth',1.5);
    axis([10^-3 10^3 0 90]);
    set(gca, 'YScale', 'linear');
    legend({'Synthetic Data','Calculated Data'},'EdgeColor','none','Color','none','FontWeight','Bold');
    xlabel('Periods (s)','FontSize',12,'FontWeight','Bold');
    ylabel('Phase (deg)','FontSize',12,'FontWeight','Bold');
    title(['\bf \fontsize{10}\fontname{Times}Period (s) vs Phase (deg)  || Misfit : ', num2str(Egen(itr)),' || iteration : ', num2str(itr)]);
    grid on
    
    subplot(2, 2, [2 4])
    stairs(rho_plot,thk_plot,'--b','Linewidth',3);
    hold on
    stairs(rhomod_plot ,thkmod_plot,'-r','Linewidth',2);
    hold off
     legend({'Synthetic Model','Calculated Model'},'EdgeColor','none','Color','none','FontWeight','Bold','Location','SouthWest');
    axis([1 10^4 0 5000]);
    xlabel('Resistivity (Ohm.m)','FontSize',12,'FontWeight','Bold');
    ylabel('Depth (m)','FontSize',12,'FontWeight','Bold');
    title(['\bf \fontsize{10}\fontname{Times}Model']);
    subtitle(['\rho_{1} = ',num2str(rho_model(1)),' || \rho_{2} = ',num2str(rho_model(2)),' || \rho_{3} = ',num2str(rho_model(3)),' || thick_{1} = ',num2str(thk_model(1)),' || thick_{2} = ',num2str(thk_model(2))],'FontWeight','bold')
    set(gca,'YDir','Reverse');
    set(gca, 'XScale', 'log');
    set(gcf, 'Position', get(0, 'Screensize'));
    grid on

    %plot misfit
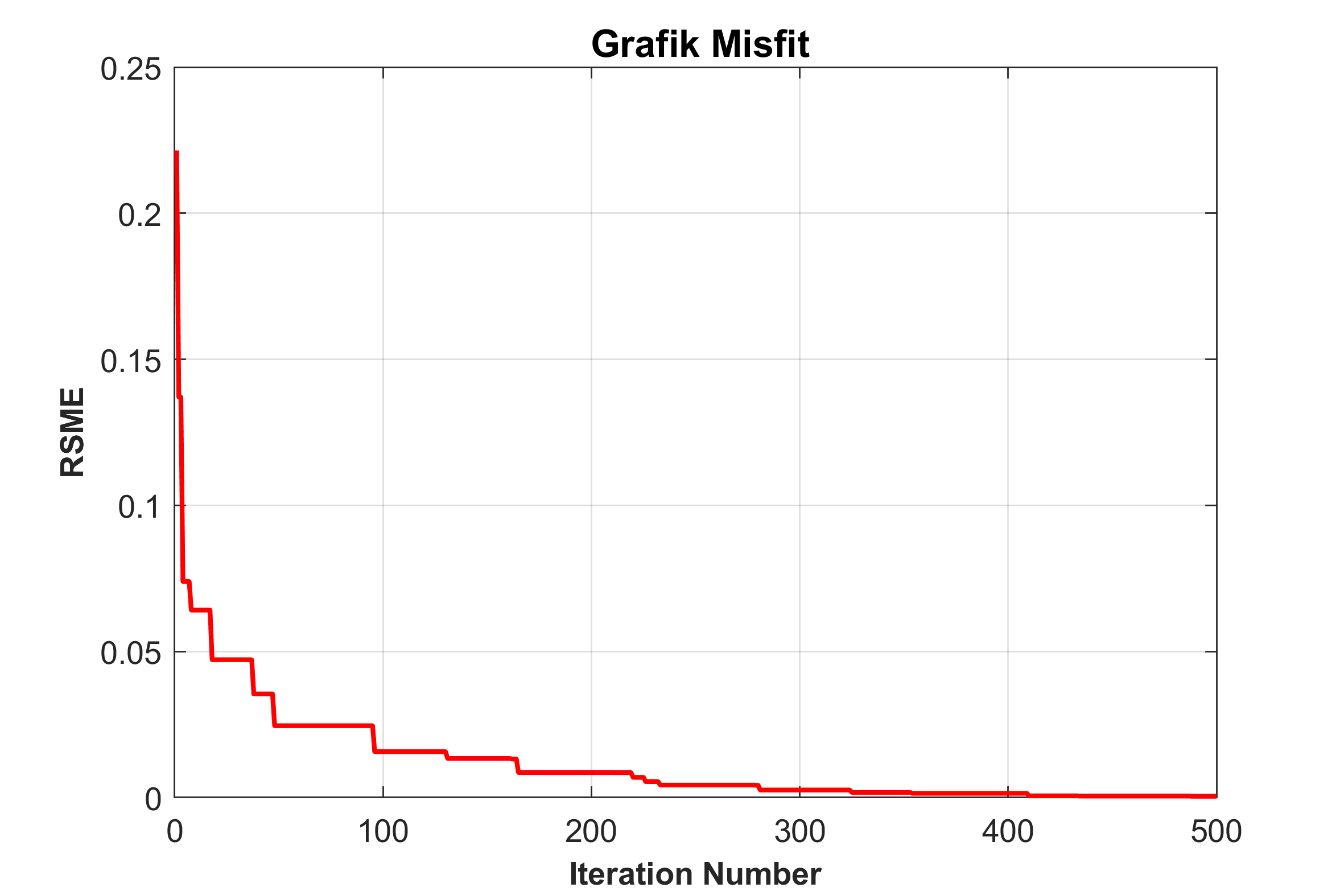
    figure(2)
    plot(1:nitr,Egen,'r','Linewidth',1.5)
    xlabel('Iteration Number','FontSize',10,'FontWeight','Bold');
    ylabel('RSME','FontSize',10,'FontWeight','Bold');
    title('\bf \fontsize{12} Grafik Misfit ');
    grid on

其中，子函数modelMT为正演函数，可参考“大地电磁一维正演”

% Digital Earth Lab
% www.DigitalEarthLab.com
% Written by Andrew Pethick 2013
% Last Updated October 29th 2013
% Licensed under WTFPL

function [apparentResistivity, phase] = modelMT(resistivities, thicknesses,period)

for k = 1 : length(period)
mu = 4*pi*1E-7; %Magnetic Permeability (H/m)  
w = 2 * pi / period(k); %Angular Frequency (Radians);
n=length(resistivities); %Number of Layers

impedances = zeros(n,1);
%Layering in this format
%  Layer     j
% Layer 1    1
% Layer 2    2
% Layer 3    3
% Layer 4    4
% Basement   5

% Steps for modelling (for each geoelectric model and frequency)
% 1. Compute basement impedance Zn using sqrt((w * mu * resistivity))
% 2. Iterate from bottom layer to top(not the basement)
    % 2.1. Calculate induction parameters
    % 2.2. Calculate Exponential factor from intrinsic impedance
    % 2.3 Calculate reflection coeficient using current layer
    %          intrinsic impedance and the below layer impedance
    
% 3. Compute apparent resistivity from top layer impedance
        %   apparent resistivity = (Zn^2)/(mu * w)

%Symbols
% Zn - Basement Impedance
% Zi - Layer Impedance
% wi - Intrinsic Impedance
% di - Induction parameter
% ei - Exponential Factor
% ri - Reflection coeficient
% re - Earth R.C.
        
%Step 1 : Calculate basement impedance  
Zn = sqrt(sqrt(-1)*w*mu*resistivities(n)); 
impedances(n) = Zn; 

%Iterate through layers starting from layer j=n-1 (i.e. the layer above the basement)        
for j = n-1:-1:1
    resistivity = resistivities(j);
    thickness = thicknesses(j);
                
    % 3. Compute apparent resistivity from top layer impedance
    %Step 2. Iterate from bottom layer to top(not the basement) 
    % Step 2.1 Calculate the intrinsic impedance of current layer
    dj = sqrt(sqrt(-1)* (w * mu * (1/resistivity)));
    wj = dj * resistivity;
        
    % Step 2.2 Calculate Exponential factor from intrinsic impedance
    ej = exp(-2*thickness*dj);                     

    % Step 2.3 Calculate reflection coeficient using current layer
    %          intrinsic impedance and the below layer impedance
    belowImpedance = impedances(j + 1);
    rj = (wj - belowImpedance)/(wj + belowImpedance); 
    re = rj*ej; 
    Zj = wj * ((1 - re)/(1 + re));
    impedances(j) = Zj;               
end
% Step 3. Compute apparent resistivity from top layer impedance
Z = impedances(1);
absZ = abs(Z); 
apparentResistivity(k) = (absZ * absZ)/(mu * w);
phase(k) = rad2deg(atan2(imag(Z),real(Z)));
end
    

子函数misfitMT如下：

function [misfit]=misfitMT(rho_obs,phase_obs,rho_cal,phase_cal)
l=length(rho_obs);
d2r=pi/180;
lamda = 0.1;
for i=1:l
    m(i)=(abs(log10(rho_cal(i)/rho_obs(i)))+abs(d2r*phase_cal(i)-d2r*phase_obs(i)));
     %m(i)=(abs(log10(rho_cal(i)/rho_obs(i)))+lamda*(abs(d2r*phase_cal(i)-d2r*phase_obs(i))));
end
misfit=sum(m)/(l);
end

FA MT1D 反演结果

左:反演模型响应对比；右:反演结果对比 FA反演过程中RMSE变化曲线

The end

@.@不方便打开Matlab？那就点击Matlab在线编辑器(Open in MATLAB Online)试一下吧。

Reference：

[1] Yang, XS. (2009). Firefly Algorithms for Multimodal Optimization. In: Watanabe, O., Zeugmann, T. (eds) Stochastic Algorithms: Foundations and Applications. SAGA 2009. Lecture Notes in Computer Science, vol 5792. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04944-6_14

Click这里直接查看该文献 P169-178

[2] CSDN回答：群体优化算法之萤火虫算法

[3] Mohammad Rheza Zamani的Github项目:1D-Magnetotelluric-Inversion之萤火虫算法