大地电磁法（Magnetotelluric，简称MT）是利用天然交变电磁信号来研究地球内部电性结构的一种方法，属于被动源地球物理方法。可参考Martyn Unsworth对MT的介绍。

这里将介绍MT一维正演的公式与matlab程序。

首先声明MT初期的两个假设：

1.平面电磁波

2.地下为水平层状均匀结构.

在这样的假设下，地球表面阻抗值$Z(\omega)$与地球的真实电阻率$\rho$可以通过下面的式子联系起来：

如果你想知道这个式子怎么来的，请点击MT1D Forward公式详细推导(各向同性)，里面有详细推导过程o.o因为本文是以编程为目的，所以为了看起来更清晰简单，正文中就尽量不放公式了~ok回到正题，上式中，

$Z(\omega)$为地球表面阻抗($\Omega$)

$\omega$为角频率(弧度)，$\omega=2\pi f$

$E_x(\omega)$为水平电场分量(V)

$H_y(\omega)$为垂直磁场分量(T)

$u_0$为真空磁导率(H/m)，$u_0=4\pi\times10^{-7}$

$\rho$为地层真实电阻率值($\Omega·m$)

如果地下只有一层的话，到这里其实就结束了-.-我们通过地球表面测得的阻抗值$Z(\omega)$直接反推就可以求得地球真实电阻率值$\rho$了。然而，地球远没有这么简单。于是，下面来介绍n层地球的情况。

LayerEarth

假设地电模型由$N$层组成，每层的电导率为$\sigma_j$，厚度为$h_j(j=1,···,N)$，第$N$层为均匀半空间，即$h_N=\infty$，那么，第$j$层(顶界面)的阻抗为：

这里，

由此可见，第$j$层(顶界面)的阻抗与第$j+1$层(顶界面)有关，因此我们需要从第$N$层开始逐层递推出第1层的阻抗$Z_1$。

最后，通过$Z_1$，我们就可以得到视电阻率和相位：

ok 所需要的公式就是这些，下面我们来介绍matlab代码。

Below is the matlab code:

首先定义一个函数MT1DForward，该函数可以计算给定频率下一维地电模型的视电阻率和相位。函数的输入为频率、地电模型的电阻率和厚度；函数的输出为视电阻率($\Omega·m$)和相位(度)

1
function [apparentRho,Phase] = MT1DForward(rho,h,f)

然后计算频率个数nFreqs和地层层数nLayer：
1
2
nFreqs = length(f);
nLayer = length(rho);

对于每一个频率，都需要计算一次响应，因此大循环为频率：
1
2
3
for iFreq = 1:nFreqs
    omega = 2*pi*f(iFreq);
    u0 = 4*pi*1e-7;

小循环为每一层地层(从第$N$层倒推第1层)：
1
2
3
4
5
6
7
8
9
10
11
for j = nLayer:-1:1
    k = sqrt(1i*omega*u0/rho(j));
    Z0 = sqrt(1i*omega*u0*rho(j));
    if j==nLayer
        Z = Z0;
        continue;
    end
    R = (Z0-Z)/(Z0+Z);
    Q = exp(-2*k*h(j));
    Z = Z0*(1-R*Q)/(1+R*Q);
end

最后计算每个频点的地表(第一层顶界面)阻抗，这里的$Z$即$Z_{j=1}$
1
Z(iFreq)=Z;

然后得到视电阻率和相位：
1
2
3
4
5
            apparentRho(iFreq) = (abs(Z(iFreq)).^2)./(omega*u0);
            Phase(iFreq) = atan2d(imag(Z(iFreq)),real(Z(iFreq))); 
            % Notice:公式里计算出的相位单位为弧度，这里为°是因为使用atan2d函数转换成了度
    end
end

如果想看看长什么样子，就试一个例子吧(记得放到上述代码的前面/重新建一个.m文件)：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function ShowMT1DForward(varargin)
f = logspace(-3,3,21)';
rho = [100;10;100];      % 三层地电模型
h = [2000;2000];         % 两个厚度(最后一层为均匀半空间)  

[apparentRho,Phase]=MT1DForward(rho,h,f);

subplot(2,1,1)
    plot(1./f,apparentRho,'o','MarkerSize',5,'MarkerFaceColor',[0,0.45,0.74])
    set(gca,'Yscale','log','Xscale','log','LineWidth',1.5,'FontSize',12)
    xlabel('periods [s]');
    ylabel('apparent \rho [\Omega m]')
    title('Rho');
    axis([10^-3,10^3,10^0,10^4]);
subplot(2,1,2)
    plot(1./f,Phase,'o','MarkerSize',5,'MarkerFaceColor',[0,0.45,0.74])
    set(gca,'Xscale','log','LineWidth',1.5,'FontSize',12)
    xlabel('periods [s]');
    ylabel('phase [\circ]');
    title('Phase');
    axis([10^-3,10^3,-inf,inf]);
end

然后你就会得到该模型的视电阻率和相位曲线咯：

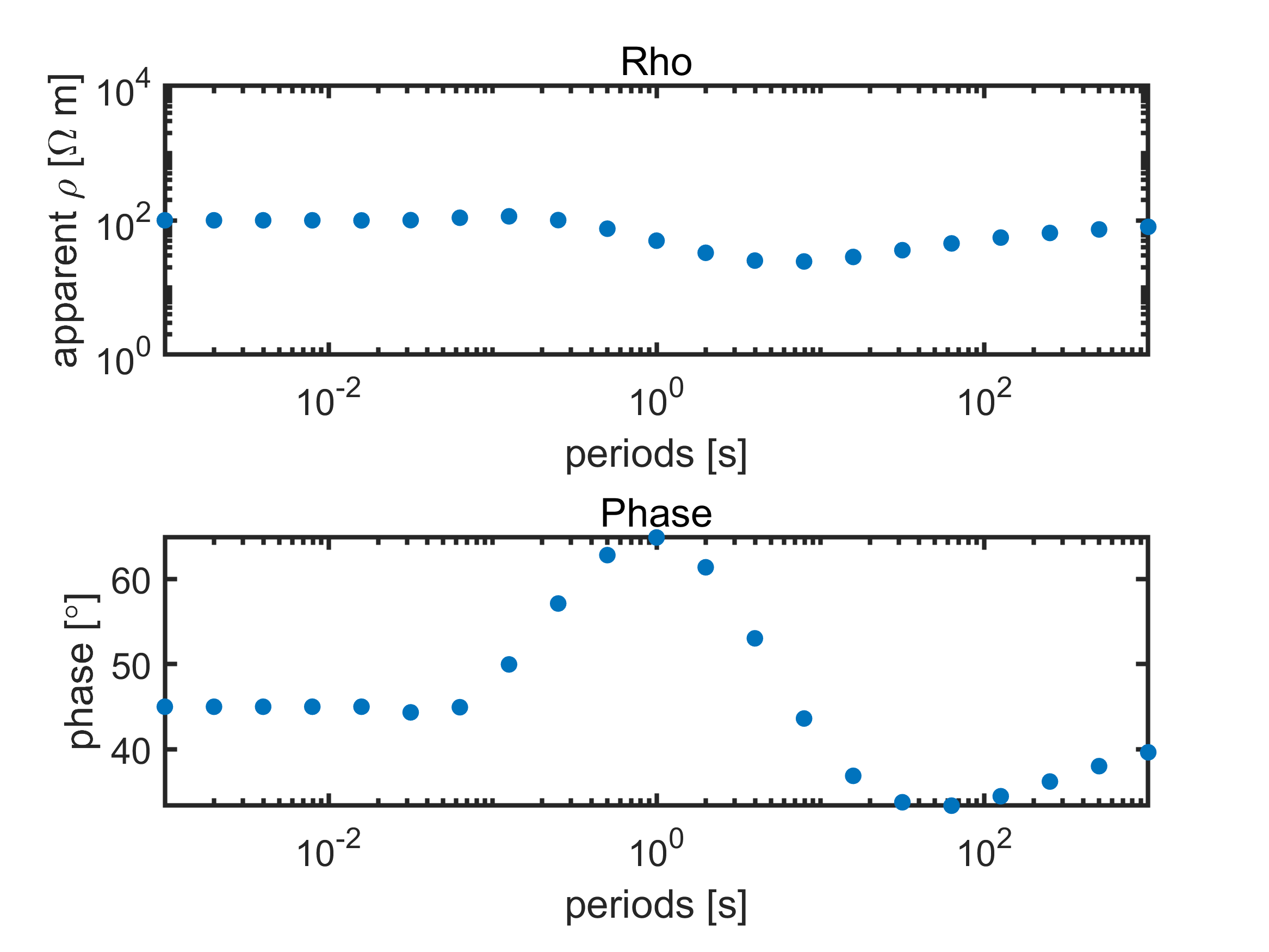
![MT1D_example](/images/PictureInsert/MT1D_ex.png)

正演结果

The end

@.@不方便打开Matlab？那就点击Matlab在线编辑器(Open in MATLAB Online)试一下吧。

Reference:

[1] 李予国老师2020年海洋电磁学课程讲义

[2] 韩波师兄MT1D_GN_inversion Code

[3] Andrew Pethick:1D Magnetotelluric Forward Modelling